Longitude
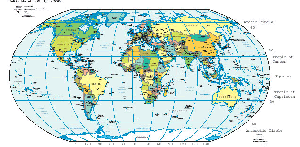
| |
| Map of Earth | |
| Longitude (λ) | |
|---|---|
| Appear curved and vertical in this projection, but are actually halves of great circles. | |
| Latitude (φ) | |
| Appear straight and horizontal in this projection, but are actually circular with different radii. All locations with a given latitude are collectively referred to as a circle of latitude. | |
| The equator divides the planet into a Northern Hemisphere and a Southern Hemisphere, and has a latitude of 0°. | |
Longitude, sometimes denoted by the Greek letter λ (lambda),[1][2] describes the location of a place on Earth east or west of a north-south line called the Prime Meridian. Longitude is given as an angular measurement ranging from 0° at the Prime Meridian to +180° eastward and −180° westward. Unlike latitude, which has the equator as a natural starting position, there is no natural starting position for longitude. Therefore, a reference meridian had to be chosen. While British cartographers had long used the Greenwich meridian in London, other references were used elsewhere, including: El Hierro, Rome, Copenhagen, Jerusalem, Saint Petersburg, Pisa, Paris, Philadelphia and Washington. In 1884, the International Meridian Conference adopted the Greenwich meridian as the universal prime meridian or zero point of longitude.
Each degree of longitude is further sub-divided into 60 minutes, each of which divided into 60 seconds. A longitude is thus specified as 23° 27′ 30" E. For high accuracy, the seconds are specified with a decimal fraction. An alternative representation uses degrees and minutes, where parts of a minute are expressed as a decimal fraction, thus: 23° 27.500′ E. Degrees may also be expressed as a decimal number: 23.45833° E. Sometimes, the West/East suffix is replaced by a negative sign for West. Confusingly, the convention of negative for East is also sometimes seen. The preferred convention that East is positive is consistent with a right-handed Cartesian coordinate system with the North Pole up.
A specific longitude may then be combined with a specific latitude to give a precise position on the Earth's surface.
As opposed to a degree of latitude, which always corresponds to exactly sixty nautical miles or about 111 km (69 statute miles, each of 5280 feet), a degree of longitude corresponds to a distance that varies from 0 to 111 km: it is 111 km times the cosine of the latitude, when the distance is laid out on a circle of constant latitude; if the shortest distance, on a great circle were used, the distance would be even a little less. More precisely, one degree of longitude = (111.320 + 0.373sin²φ)cosφ km, where φ is latitude).[3]
Longitude at a point may be determined by calculating the time difference between that at its location and Coordinated Universal Time (UTC). Since there are 24 hours in a day and 360 degrees in a circle, the sun moves across the sky at a rate of 15 degrees per hour (360°/24 hours = 15° per hour). So if the time zone a person is in is three hours ahead of UTC then that person is near 45° longitude (3 hours × 15° per hour = 45°). The word near was used because the point might not be at the center of the time zone; also the time zones are defined politically, so their centers and boundaries often do not lie on meridians at multiples of 15°. In order to perform this calculation, however, a person needs to have a chronometer (watch) set to UTC and needs to determine local time by solar observation or astronomical observation. The details are more complex than described here: see the articles on Universal Time and on the Equation of time for more details.
A line of constant longitude is a meridian, and half of a great circle.
History of the measurement of longitude
The search for a solution
The measurement of longitude is important to both cartography and navigation. Historically, the most important practical application of these was to provide safe ocean navigation. Knowledge of both latitude and longitude was required. Whereas latitude was easy to determine by celestial navigation using the elevation of the pole star or of the sun at noon, for longitude early ocean navigators had to rely on dead reckoning. This was inaccurate on long voyages out of sight of land, and these voyages sometimes ended with shipwrecks.
The discovery of how to measure longitude accurately was among the important discoveries of the 1600s and 1700s. The first effective solution for mapmaking was achieved by Giovanni Domenico Cassini starting in 1681, using Galileo's method based on the satellites of Jupiter. For application without a professional astronomer at hand, and in particular measurement at sea, the problem was more difficult; see Dava Sobel's book: Longitude: The True Story of a Lone Genius Who Solved the Greatest Scientific Problem of His Time for a good historical overview. This genius was John Harrison.
Longitude Act and Harrison's chronometer
The tragic wrecking of the British fleet led by Sir Cloudesley Shovell led to the British Longitude Act, which created the Longitude Prize for anyone who could devise a practical method of determining longitude at sea. This was eventually achieved by John Harrison with his chronometer; the timepiece in question was the one later known as H-4.
Harrison's son led a voyage aboard a ship from Portsmouth, England to the Caribbean port city of Bridgetown, Barbados with the H-4 aboard. Harrison demonstrated a method of determining longitude by keeping the exact time of day for Britain, while using astronomical observations to find the exact local time on the ship as it sailed to the island of Barbados. In this way he was able to determine the position of the ship relative to Barbados whose longitude was known. The calculation of the ship's position was only 10 miles in error when it arrived.
Today, by other means, we can know the exact time in London (Greenwich Mean Time, Universal Coordinated Time, or "Zulu" Time). By noting the local noon time anywhere in the world, that is, when the sun crosses your meridian (and this can be done quite precisely with a long plumb bob on land), correcting for the Equation of Time, and comparing it with GMT, one's local longitude can be calculated quite accurately. This is the fundamental principle of Harrison's H-4 chronometer, which for use on a sea-going vessel could not use a pendulum. More than anything, this invention marked a breakthrough in clock precision.
Later developments
Exchanges of chronometers between observatories, to determine the precise differences in local time, used in conjunction with the observation of the transit of stars across the meridian became a standard way of determining longitude. Another method was the observation of occultations of stars at different observatories. From the mid 19th century, instead of exchanging chronometers, telegraph time signals were used; radio time signals followed in the early 20th century. Satellites were used for measurements from the 1970s and 1980s - see GPS.
Longitude is the second part of the ICBM address, latitude being the first.
Ecliptic latitude and longitude
Ecliptic latitude and longitude are defined for the planets, stars, and other celestial bodies in a similar way to that in which the terrestrial counterparts are defined. The pole is the normal to the ecliptic nearest to the celestial north pole. Ecliptic latitude is measured from 0° to 90° north (+) or south (−) of the ecliptic. Ecliptic longitude is measured from 0° to 360° eastward (the direction that the Sun appears to move relative to the stars) along the ecliptic from the vernal equinox. The equinox at a specific date and time is a fixed equinox, such as that in the J2000 reference frame.
However, the equinox moves because it is the intersection of two planes, both of which move. The ecliptic is relatively stationary, wobbling within a 4° diameter circle relative to the fixed stars over millions of years under the gravitational influence of the other planets. The greatest movement is a relatively rapid gyration of Earth's equatorial plane whose pole traces a 47° diameter circle caused by the Moon. This causes the equinox to precess westward along the ecliptic about 50" per year. This moving equinox is called the equinox of date. Ecliptic longitude relative to a moving equinox is used whenever the positions of the Sun, Moon, planets, or stars at dates other than that of a fixed equinox is important, as in calendars, astrology, or celestial mechanics. The 'error' of the Julian or Gregorian calendar is always relative to a moving equinox. The years, months, and days of the Chinese calendar all depend on the ecliptic longitudes of date of the Sun and Moon. The 30° zodiacal segments used in astrology are also relative to a moving equinox. Celestial mechanics (here restricted to the motion of solar system bodies) uses both a fixed and moving equinox. Sometimes in the study of Milankovitch cycles, the invariable plane of the solar system is substituted for the moving ecliptic. Longitude may be denominated from 0 to \(\begin{matrix}2\pi\end{matrix}\) radians in either case.
Longitude on bodies other than Earth
Planetary co-ordinate systems are defined relative to their mean axis of rotation and various definitions of longitude depending on the body. The longitude systems of most of those bodies with observable rigid surfaces have been defined by references to a surface feature such as a crater. The north pole is that pole of rotation that lies on the north side of the invariable plane of the solar system (the ecliptic). The location of the prime meridian as well as the position of body's north pole on the celestial sphere may vary with time due to precession of the axis of rotation of the planet (or satellite). If the position angle of the body's prime meridian increases with time, the body has a direct (or prograde) rotation; otherwise the rotation is said to be retrograde.
In the absence of other information, the axis of rotation is assumed to be normal to the mean orbital plane; Mercury and most of the satellites are in this category. For many of the satellites, it is assumed that the rotation rate is equal to the mean orbital period. In the case of the giant planets, since their surface features are constantly changing and moving at various rates, the rotation of their magnetic fields is used as a reference instead. In the case of the Sun, even this criterion fails (because its magnetosphere is very complex and does not really rotate in a steady fashion), and an agreed-upon value for the rotation of its equator is used instead.
For "planetographic longitude", west longitudes (i.e., longitudes measured positively to the west) are used when the rotation is prograde and east longitudes (i.e., longitudes measured positively to the east) when the rotation is retrograde. However, "planetocentric longitude" is measured positively to the east. Because of tradition, the Earth, Sun, and Moon do not conform with this definition: their rotations are prograde and longitudes run both east and west 180° instead of the usual 360°.
The reference surfaces for some planets (such as Earth and Mars) are ellipsoids of revolution for which the equatorial radius is larger than the polar radius. Smaller bodies (Io, Mimas, etc.) tend to be better approximated by triaxial ellipsoids; however, triaxial ellipsoids would render many computations more complicated, especially those related to map projections. Many projections would lose their elegant and popular properties. For this reason spherical reference surfaces are frequently used in mapping programs.
The modern standard for maps of Mars (since about 2002) is to use planetocentric coordinates. The meridian of Mars is located at Airy-0 crater.[4]
Notes
- ^ Coordinate Conversion
- ^ "λ = Longitude east of Greenwich (for longitude west of Greenwich, use a minus sign)."
John P. Snyder, Map Projections, A Working Manual, USGS Professional Paper 1395, page ix - ^ P. Kenneth Seidelmann, ed., Explanatory Supplement to the Astronomical Almanac (Mill Valley, Cal.: University Science Books, 1992) page 700.
- ^ Where is zero degrees longitude on Mars?
See also
- Celestial navigation
- Dead reckoning
- Geodetic system
- Geographic coordinate system
- Great-circle distance explains how to find that quantity if one knows the two latitudes and longitudes.
- Navigation
- Sextant
- Time zone
- Latitude
External links
- Resources for determining your latitude and longitude
- Worldwide Index - Tageo.com – contains 2,700,000 coordinates of places including US towns
- for each city it gives the satellite map location, country, province, coordinates (dd,dms), variant names and nearby places.
- PBS Nova Online: Lost at Sea, the Search for Longitude
- IAU/IAG Working Group On Cartographic Coordinates and Rotational Elements of the Planets and Satellites
- Latitude and longitude converter – Convert latitude and longitude from degree, decimal form to degree, minutes, seconds form and vice versa. Also included a farthest point and a distance calculator.