Directory talk:Jon Awbrey/Papers/Differential Logic : Introduction
Work Area • Logical Cacti
- Theme One Program — Logical Cacti
- http://stderr.org/pipermail/inquiry/2005-February/thread.html#2348
- http://stderr.org/pipermail/inquiry/2005-February/002360.html
- http://stderr.org/pipermail/inquiry/2005-February/002361.html
Original Version
Up till now we've been working to hammer out a two-edged sword of syntax, honing the syntax of painted and rooted cacti and expressions (PARCAE), and turning it to use in taming the syntax of two-level formal languages.
But the purpose of a logical syntax is to support a logical semantics, which means, for starters, to bear interpretation as sentential signs that can denote objective propositions about some universe of objects.
One of the difficulties that we face in this discussion is that the words interpretation, meaning, semantics, and so on will have so many different meanings from one moment to the next of their use. A dedicated neologician might be able to think up distinctive names for all of the aspects of meaning and all of the approaches to them that will concern us here, but I will just have to do the best that I can with the common lot of ambiguous terms, leaving it to context and the intelligent interpreter to sort it out as much as possible.
As it happens, the language of cacti is so abstract that it can bear at least two different interpretations as logical sentences denoting logical propositions. The two interpretations that I know about are descended from the ones that Charles Sanders Peirce called the entitative and the existential interpretations of his systems of graphical logics. For our present aims, I shall briefly introduce the alternatives and then quickly move to the existential interpretation of logical cacti.
Table A illustrates the existential interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.
| \(\text{Cactus Graph}\!\) | \(\text{Cactus Expression}\!\) | \(\text{Interpretation}\!\) |
|
\({}^{\backprime\backprime}\texttt{~}{}^{\prime\prime}\) | \(\operatorname{true}.\) |
|
\(\texttt{(~)}\) | \(\operatorname{false}.\) |
|
\(a\!\) | \(a.\!\) |
_Big.jpg){kind=small}
|
\(\texttt{(} a \texttt{)}\) |
\(\begin{matrix} \tilde{a} \\[2pt] a^\prime \\[2pt] \lnot a \\[2pt] \operatorname{not}~ a. \end{matrix}\) |
|
\(a~b~c\) |
\(\begin{matrix} a \land b \land c \\[6pt] a ~\operatorname{and}~ b ~\operatorname{and}~ c. \end{matrix}\) |
(B)(C))_Big.jpg)
|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\) |
\(\begin{matrix} a \lor b \lor c \\[6pt] a ~\operatorname{or}~ b ~\operatorname{or}~ c. \end{matrix}\) |
)_Big.jpg)
|
\(\texttt{(} a \texttt{(} b \texttt{))}\) |
\(\begin{matrix} a \Rightarrow b \\[2pt] a ~\operatorname{implies}~ b. \\[2pt] \operatorname{if}~ a ~\operatorname{then}~ b. \\[2pt] \operatorname{not}~ a ~\operatorname{without}~ b. \end{matrix}\) |
_Big.jpg)
|
\(\texttt{(} a \texttt{,} b \texttt{)}\) |
\(\begin{matrix} a + b \\[2pt] a \neq b \\[2pt] a ~\operatorname{exclusive-or}~ b. \\[2pt] a ~\operatorname{not~equal~to}~ b. \end{matrix}\) |
)_Big.jpg)
|
\(\texttt{((} a \texttt{,} b \texttt{))}\) |
\(\begin{matrix} a = b \\[2pt] a \iff b \\[2pt] a ~\operatorname{equals}~ b. \\[2pt] a ~\operatorname{if~and~only~if}~ b. \end{matrix}\) |
_Big.jpg)
|
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\) |
\(\begin{matrix} \operatorname{just~one~of} \\ a, b, c \\ \operatorname{is~false}. \end{matrix}\) |
,(B),(C))_Big.jpg)
|
\(\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}\) |
\(\begin{matrix} \operatorname{just~one~of} \\ a, b, c \\ \operatorname{is~true}. \end{matrix}\) |
,(C))_Big.jpg)
|
\(\texttt{(} a \texttt{,(} b \texttt{),(} c \texttt{))}\) |
\(\begin{matrix} \operatorname{genus}~ a ~\operatorname{of~species}~ b, c. \\[6pt] \operatorname{partition}~ a ~\operatorname{into}~ b, c. \\[6pt] \operatorname{pie}~ a ~\operatorname{of~slices}~ b, c. \end{matrix}\) |
Table B illustrates the entitative interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.
| \(\text{Cactus Graph}\!\) | \(\text{Cactus Expression}\!\) | \(\text{Interpretation}\!\) |
|
|
\({}^{\backprime\backprime}\texttt{~}{}^{\prime\prime}\) | \(\operatorname{false}.\) |
|
|
\(\texttt{(~)}\) | \(\operatorname{true}.\) |
|
|
\(a\!\) | \(a.\!\) |
|
|
\(\texttt{(} a \texttt{)}\) |
\(\begin{matrix} \tilde{a} \\[2pt] a^\prime \\[2pt] \lnot a \\[2pt] \operatorname{not}~ a. \end{matrix}\) |
|
|
\(a~b~c\) |
\(\begin{matrix} a \lor b \lor c \\[6pt] a ~\operatorname{or}~ b ~\operatorname{or}~ c. \end{matrix}\) |
|
|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\) |
\(\begin{matrix} a \land b \land c \\[6pt] a ~\operatorname{and}~ b ~\operatorname{and}~ c. \end{matrix}\) |
B_Big.jpg){kind=small}
|
\(\texttt{(} a \texttt{)} b\) |
\(\begin{matrix} a \Rightarrow b \\[2pt] a ~\operatorname{implies}~ b. \\[2pt] \operatorname{if}~ a ~\operatorname{then}~ b. \\[2pt] \operatorname{not}~ a, ~\operatorname{or}~ b. \end{matrix}\) |
|
|
\(\texttt{(} a \texttt{,} b \texttt{)}\) |
\(\begin{matrix} a = b \\[2pt] a \iff b \\[2pt] a ~\operatorname{equals}~ b. \\[2pt] a ~\operatorname{if~and~only~if}~ b. \end{matrix}\) |
|
|
\(\texttt{((} a \texttt{,} b \texttt{))}\) |
\(\begin{matrix} a + b \\[2pt] a \neq b \\[2pt] a ~\operatorname{exclusive-or}~ b. \\[2pt] a ~\operatorname{not~equal~to}~ b. \end{matrix}\) |
|
|
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\) |
\(\begin{matrix} \operatorname{not~just~one~of} \\ a, b, c \\ \operatorname{is~true}. \end{matrix}\) |
)_Big.jpg)
|
\(\texttt{((} a \texttt{,} b \texttt{,} c \texttt{))}\) |
\(\begin{matrix} \operatorname{just~one~of} \\ a, b, c \\ \operatorname{is~true}. \end{matrix}\) |
,B,C))_Big.jpg)
|
\(\texttt{(((} a \texttt{),} b \texttt{,} c \texttt{))}\) |
\(\begin{matrix} \operatorname{genus}~ a ~\operatorname{of~species}~ b, c. \\[6pt] \operatorname{partition}~ a ~\operatorname{into}~ b, c. \\[6pt] \operatorname{pie}~ a ~\operatorname{of~slices}~ b, c. \end{matrix}\) |
For the time being, the main things to take away from Tables A and B are the ideas that the compositional structure of cactus graphs and expressions can be articulated in terms of two different kinds of connective operations, and that there are two distinct ways of mapping this compositional structure into the compositional structure of propositional sentences, say, in English:
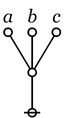
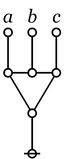
| 1. | The node connective joins a number of component cacti \(C_1, \ldots, C_k\) at a node: |
C_1 ... C_k
@
| |
| 2. | The lobe connective joins a number of component cacti \(C_1, \ldots, C_k\) to a lobe: |
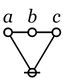
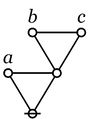
C_1 C_2 C_k
o---o-...-o
\ /
\ /
\ /
\ /
@
|
Table 15 summarizes the existential and entitative interpretations of the primitive cactus structures, in effect, the graphical constants and connectives.
Table 15. Existential & Entitative Interpretations of Cactus Structures o-----------------o-----------------o-----------------o-----------------o | Cactus Graph | Cactus String | Existential | Entitative | | | | Interpretation | Interpretation | o-----------------o-----------------o-----------------o-----------------o | | | | | | @ | " " | true | false | | | | | | o-----------------o-----------------o-----------------o-----------------o | | | | | | o | | | | | | | | | | | @ | ( ) | false | true | | | | | | o-----------------o-----------------o-----------------o-----------------o | | | | | | C_1 ... C_k | | | | | @ | C_1 ... C_k | C_1 & ... & C_k | C_1 v ... v C_k | | | | | | o-----------------o-----------------o-----------------o-----------------o | | | | | | C_1 C_2 C_k | | Just one | Not just one | | o---o-...-o | | | | | \ / | | of the C_j, | of the C_j, | | \ / | | | | | \ / | | j = 1 to k, | j = 1 to k, | | \ / | | | | | @ | (C_1, ..., C_k) | is not true. | is true. | | | | | | o-----------------o-----------------o-----------------o-----------------o |
It is possible to specify abstract rules of equivalence (AROEs) between cacti, rules for transforming one cactus into another that are formal in the sense of being indifferent to the above choices for logical or semantic interpretations, and that partition the set of cacti into formal equivalence classes.
A reduction is an equivalence transformation that is applied in the direction of decreasing graphical complexity.
A basic reduction is a reduction that applies to one of the two families of basic connectives.
Table 16 schematizes the two types of basic reductions in a purely formal, interpretation-independent fashion.
Table 16. Basic Reductions o---------------------------------------o | | | C_1 ... C_k | | @ = @ | | | | if and only if | | | | C_j = @ for all j = 1 to k | | | o---------------------------------------o | | | C_1 C_2 C_k | | o---o-...-o | | \ / | | \ / | | \ / | | \ / | | @ = @ | | | | if and only if | | | | o | | | | | C_j = @ for exactly one j in [1, k] | | | o---------------------------------------o |
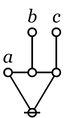
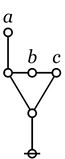
The careful reader will have noticed that we have begun to use graphical paints like "a", "b", "c" and schematic proxies like "C_1", "C_j", "C_k" in a variety of novel and unjustified ways.
The careful writer would have already introduced a whole bevy of technical concepts and proved a whole crew of formal theorems to justify their use before contemplating this stage of development, but I have been hurrying to proceed with the informal exposition, and this expedition must leave steps to the reader's imagination.
Of course I mean the active imagination. So let me assist the prospective exercise with a few hints of what it would take to guarantee that these practices make sense.
Partial Rewrites
Table 13 illustrates the existential interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.
Even though I do most of my thinking in the existential interpretation, I will continue to speak of these forms as logical graphs, because I think it is an important fact about them that the formal validity of the axioms and theorems is not dependent on the choice between the entitative and the existential interpretations.
The first extension is the reflective extension of logical graphs (RefLog). It is obtained by generalizing the negation operator "\(\texttt{(~)}\)" in a certain way, calling "\(\texttt{(~)}\)" the controlled, moderated, or reflective negation operator of order 1, then adding another such operator for each finite \(k = 2, 3, \ldots .\)
In sum, these operators are symbolized by bracketed argument lists as follows: "\(\texttt{(~)}\)", "\(\texttt{(~,~)}\)", "\(\texttt{(~,~,~)}\)", …, where the number of slots is the order of the reflective negation operator in question.
The cactus graph and the cactus expression shown here are both described as a spike.
o---------------------------------------o | | | o | | | | | @ | | | o---------------------------------------o | ( ) | o---------------------------------------o |
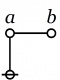
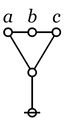
The rule of reduction for a lobe is:
o---------------------------------------o | | | x_1 x_2 ... x_k | | o-----o--- ... ---o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ = @ | | | o---------------------------------------o |
if and only if exactly one of the \(x_j\!\) is a spike.
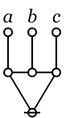
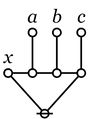
In Ref Log, an expression of the form \(\texttt{((}~ e_1 ~\texttt{),(}~ e_2 ~\texttt{),(}~ \ldots ~\texttt{),(}~ e_k ~\texttt{))}\) expresses the fact that exactly one of the \(e_j\!\) is true. Expressions of this form are called universal partition expressions, and they parse into a type of graph called a painted and rooted cactus (PARC):
o---------------------------------------o | | | e_1 e_2 ... e_k | | o o o | | | | | | | o-----o--- ... ---o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o |
o---------------------------------------o | | | ( x1, x2, ..., xk ) = [blank] | | | | iff | | | | Just one of the arguments | | x1, x2, ..., xk = () | | | o---------------------------------------o |
The interpretation of these operators, read as assertions about the values of their listed arguments, is as follows:
| Existential Interpretation: | Just one of the k argument is false. |
| Entitative Interpretation: | Not just one of the k arguments is true. |
Tables
| \(\text{Graph}\!\) | \(\text{Expression}\!\) | \(\text{Interpretation}\!\) | \(\text{Other Notations}\!\) |
|
|
\(~\) | \(\operatorname{true}\) | \(1\!\) |
|
|
\(\texttt{(~)}\) | \(\operatorname{false}\) | \(0\!\) |
|
|
\(a\!\) | \(a\!\) | \(a\!\) |
|
|
\(\texttt{(} a \texttt{)}\) | \(\operatorname{not}~ a\) | \(\lnot a \quad \bar{a} \quad \tilde{a} \quad a^\prime\) |
|
|
\(a ~ b ~ c\) | \(a ~\operatorname{and}~ b ~\operatorname{and}~ c\) | \(a \land b \land c\) |
|
|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\) | \(a ~\operatorname{or}~ b ~\operatorname{or}~ c\) | \(a \lor b \lor c\) |
|
|
\(\texttt{(} a \texttt{(} b \texttt{))}\) |
\(\begin{matrix} a ~\operatorname{implies}~ b \\[6pt] \operatorname{if}~ a ~\operatorname{then}~ b \end{matrix}\) |
\(a \Rightarrow b\) |
|
|
\(\texttt{(} a \texttt{,} b \texttt{)}\) |
\(\begin{matrix} a ~\operatorname{not~equal~to}~ b \\[6pt] a ~\operatorname{exclusive~or}~ b \end{matrix}\) |
\(\begin{matrix} a \neq b \\[6pt] a + b \end{matrix}\) |
|
|
\(\texttt{((} a \texttt{,} b \texttt{))}\) |
\(\begin{matrix} a ~\operatorname{is~equal~to}~ b \\[6pt] a ~\operatorname{if~and~only~if}~ b \end{matrix}\) |
\(\begin{matrix} a = b \\[6pt] a \Leftrightarrow b \end{matrix}\) |
|
|
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\) |
\(\begin{matrix} \operatorname{just~one~of} \\ a, b, c \\ \operatorname{is~false}. \end{matrix}\) |
\(\begin{matrix} & \bar{a} ~ b ~ c \\ \lor & a ~ \bar{b} ~ c \\ \lor & a ~ b ~ \bar{c} \end{matrix}\) |
|
|
\(\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}\) |
\(\begin{matrix} \operatorname{just~one~of} \\ a, b, c \\ \operatorname{is~true}. \\[6pt] \operatorname{partition~all} \\ \operatorname{into}~ a, b, c. \end{matrix}\) |
\(\begin{matrix} & a ~ \bar{b} ~ \bar{c} \\ \lor & \bar{a} ~ b ~ \bar{c} \\ \lor & \bar{a} ~ \bar{b} ~ c \end{matrix}\) |
)_Big.jpg)
|
\(\texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))}\) |
\(\begin{matrix} \operatorname{oddly~many~of} \\ a, b, c \\ \operatorname{are~true}. \end{matrix}\) |
\(a + b + c\!\)
\(\begin{matrix} & a ~ b ~ c \\ \lor & a ~ \bar{b} ~ \bar{c} \\ \lor & \bar{a} ~ b ~ \bar{c} \\ \lor & \bar{a} ~ \bar{b} ~ c \end{matrix}\) |
,(B),(C))_Big.jpg)
|
\(\texttt{(} x \texttt{,(} a \texttt{),(} b \texttt{),(} c \texttt{))}\) |
\(\begin{matrix} \operatorname{partition}~ x \\ \operatorname{into}~ a, b, c. \\[6pt] \operatorname{genus}~ x ~\operatorname{comprises} \\ \operatorname{species}~ a, b, c. \end{matrix}\) |
\(\begin{matrix} & \bar{x} ~ \bar{a} ~ \bar{b} ~ \bar{c} \\ \lor & x ~ a ~ \bar{b} ~ \bar{c} \\ \lor & x ~ \bar{a} ~ b ~ \bar{c} \\ \lor & x ~ \bar{a} ~ \bar{b} ~ c \end{matrix}\) |
| \(\text{Graph}\!\) | \(\text{String}\!\) | \(\text{Existential}\!\) | \(\text{Entitative}\!\) |
|
|
\({}^{\backprime\backprime}\texttt{~}{}^{\prime\prime}\) | \(\operatorname{true}.\) | \(\operatorname{false}.\) |
|
|
\(\texttt{(~)}\) | \(\operatorname{false}.\) | \(\operatorname{true}.\) |
|
|
\(a\!\) | \(a.\!\) | \(a.\!\) |
|
|
\(\texttt{(} a \texttt{)}\) | \(\lnot a\) | \(\lnot a\) |
|
|
\(a~b~c\) | \(a \land b \land c\) | \(a \lor b \lor c\) |
|
|
\(\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}\) | \(a \lor b \lor c\) | \(a \land b \land c\) |
|
|
\(\texttt{(} a \texttt{(} b \texttt{))}\) | \(a \Rightarrow b\) | |
|
|
\(\texttt{(} a \texttt{)} b\) | \(a \Rightarrow b\) | |
|
|
\(\texttt{(} a \texttt{,} b \texttt{)}\) | \(a \neq b\) | \(a = b\!\) |
|
|
\(\texttt{((} a \texttt{,} b \texttt{))}\) | \(a = b\!\) | \(a \neq b\!\) |
|
|
\(\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}\) |
\(\begin{matrix} \operatorname{just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~false}. \end{matrix}\) |
\(\begin{matrix} \operatorname{not~just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~true}. \end{matrix}\) |
|
|
\(\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}\) |
\(\begin{matrix} \operatorname{just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~true}. \end{matrix}\) |
\(\begin{matrix} \operatorname{not~just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~false}. \end{matrix}\) |
|
|
\(\texttt{((} a \texttt{,} b \texttt{,} c \texttt{))}\) |
\(\begin{matrix} \operatorname{not~just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~false}. \end{matrix}\) |
\(\begin{matrix} \operatorname{just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~true}. \end{matrix}\) |
,(B),(C)))_Big.jpg)
|
\(\texttt{(((} a \texttt{),(} b \texttt{),(} c \texttt{)))}\) |
\(\begin{matrix} \operatorname{not~just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~true}. \end{matrix}\) |
\(\begin{matrix} \operatorname{just~one} \\ \operatorname{of}~ a, b, c \\ \operatorname{is~false}. \end{matrix}\) |
|
|
\(\texttt{(} a \texttt{,(} b \texttt{),(} c \texttt{))}\) |
\(\begin{matrix} \operatorname{partition}~ a \\ \operatorname{into}~ b, c. \end{matrix}\) |
|
|
|
\(\texttt{(((} a \texttt{),} b \texttt{,} c \texttt{))}\) |
\(\begin{matrix} \operatorname{partition}~ a \\ \operatorname{into}~ b, c. \end{matrix}\) |
