Differential Logic and Dynamic Systems • Part 2
Author: Jon Awbrey
• Overview • Part 1 • Part 2 • Part 3 • Part 4 • Part 5 • Appendices • References • Document History •
Back to the Beginning • Exemplary Universes
|
I would have preferred to be enveloped in words, borne way beyond all possible beginnings. |
||
| — Michel Foucault, The Discourse on Language, [Fou, 215] | ||
To anchor our understanding of differential logic let's look at how the various concepts apply in the simplest possible concrete cases, where the initial dimension is only 1 or 2. In spite of the simplicity of those cases it is possible to observe how central difficulties of the subject begin to arise already at that stage.
A One‑Dimensional Universe
|
There was never any more inception than there is now, | |
| — Walt Whitman, Leaves of Grass, [Whi, 28] |
Let \(\mathcal{X} = \{ A \}\) be a logical basis containing one boolean variable or logical feature \(A.\) The basis element \(A\) may be regarded as a simple proposition or coordinate projection \(A : \mathbb{B} \to \mathbb{B}.\) Corresponding to the basis \(\mathcal{X} = \{ A \}\) is the alphabet \(\mathfrak{X} = \{ \text{“} A \text{”} \}\) which serves whenever we need to make explicit mention of the symbols used in our formulas and representations.
The space \(X = \langle A \rangle = \{ \texttt{(} A \texttt{)}, A \}\) of points (cells, vectors, interpretations) has cardinality \(2^n = 2^1 = 2\) and is isomorphic to \(\mathbb{B} = \{ 0, 1 \}.\) Moreover, \(X\) may be identified with the set of singular propositions \(\{ x : \mathbb{B} \xrightarrow{s} \mathbb{B} \}.\)
The space of linear propositions \(X^* = \{ \mathrm{hom} : \mathbb{B} \xrightarrow{\ell} \mathbb{B} \} = \{ 0, A \}\) is algebraically dual to \(X\) and also has cardinality \(2.\) Here, \({}^{\backprime\backprime} 0 {}^{\prime\prime}\) is interpreted as denoting the constant function \(0 : \mathbb{B} \to \mathbb{B},\) amounting to the linear proposition of rank \(0,\) while \(A\) is the linear proposition of rank \(1.\)
Last but not least we have the positive propositions \(\{ \mathrm{pos} : \mathbb{B} \xrightarrow{p} \mathbb{B} \} = \{ A, 1 \}\) of rank \(1\) and \(0,\) respectively, where \({}^{\backprime\backprime} 1 {}^{\prime\prime}\) is understood as denoting the constant function \(1 : \mathbb{B} \to \mathbb{B}.\)
All told there are \(2^{2^n} = 2^{2^1} = 4\) propositions in the universe of discourse \(\mathcal{X}^\bullet = [\mathcal{X}],\) collectively forming the set \(X^\uparrow = \{ f : X \to \mathbb{B} \} = \{ 0, \texttt{(} A \texttt{)}, A, 1 \} \cong (\mathbb{B} \to \mathbb{B}).\)
The first order differential extension of \(\mathcal{X}\) is \(\mathrm{E}\mathcal{X} = \{ x_1, \mathrm{d}x_1 \} = \{ A, \mathrm{d}A \}.\) If the feature \(A\) is interpreted as applying to some object or state then the feature \(\mathrm{d}A\) may be taken as an attribute of the same object or state which tells it is changing significantly with respect to the property \(A,\) as if it bore an “escape velocity” with respect to the state \(A.\) In practice, differential features acquire their meaning through a class of temporal inference rules.
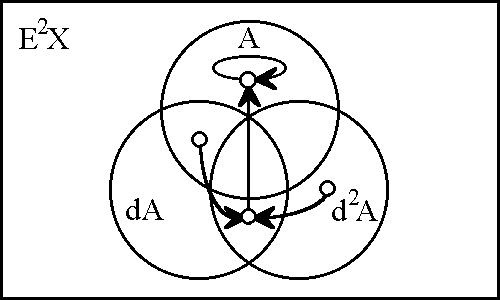
For example, relative to a frame of observation to be left implicit for now, if \(A\) and \(\mathrm{d}A\) are true at a given moment, it would be reasonable to assume \(\texttt{(} A \texttt{)}\) will be true in the next moment of observation. Taken all together we have the fourfold scheme of inference shown below.
| 600px |
|
The clock indicates the moment . . . . but what does | |
| — Walt Whitman, Leaves of Grass, [Whi, 79] |
It might be thought an independent time variable needs to be brought in at this point but it is an insight of fundamental importance to recognize the idea of process is logically prior to the notion of time. A time variable is a reference to a clock — a canonical, conventional process accepted or established as a standard of measurement but in essence no different than any other process. This raises the question of how different subsystems in a more global process can be brought into comparison and what it means for one process to serve the function of a local standard for others. But inquiries of that order serve but to wrap up puzzles in further riddles and are obviously too involved to be handled at our current level of approximation.
Observe how the secular inference rules, used by themselves, involve a loss of information, since nothing in them tells whether the momenta \(\{ \texttt{(} \mathrm{d}A \texttt{)}, \mathrm{d}A \}\) are changed or unchanged in the next moment. To know that one would have to determine \(\mathrm{d}^2 A,\) and so on, pursuing an infinite regress. In order to rest with a finitely determinate system it is necessary to make an infinite assumption, for example, that \(\mathrm{d}^k A = 0\) for all \(k\) greater than some fixed value \(M.\) Another way to escape the regress is through the provision of a dynamic law, in typical form making higher order differentials dependent on lower degrees and estates.
Example 1. A Square Rigging
|
Urge and urge and urge, | |
| — Walt Whitman, Leaves of Grass, [Whi, 28] |
Returning to the universe of discourse based on a single feature \(A,\) suppose we are given the initial condition \(A = \mathrm{d}A\) and the second order differential law \(\mathrm{d}^2 A = \texttt{(} A \texttt{)}.\) Since the equation \(A = \mathrm{d}A\) is logically equivalent to the disjunction \(A ~ \mathrm{d}A \lor \texttt{(} A \texttt{)(} \mathrm{d}A \texttt{)}\) we may infer two possible trajectories, as shown in Table 11. In either case the state \(A ~ \texttt{(} \mathrm{d}A \texttt{)(} \mathrm{d}^2 A \texttt{)}\) is a stable attractor or terminal condition for both starting points.
| \(\text{Time}\) | \(\text{Trajectory 1}\) | \(\text{Trajectory 2}\) |
|
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 2 \\[4pt] 3 \\[4pt] 4 \end{matrix}\) |
\(\begin{matrix} A & \mathrm{d}A & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] \texttt{(} A \texttt{)} & \mathrm{d}A & \mathrm{d}^2 A \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] {}^{\shortparallel} & {}^{\shortparallel} & {}^{\shortparallel} \end{matrix}\) |
\(\begin{matrix} \texttt{(} A \texttt{)} & \texttt{(} \mathrm{d}A \texttt{)} & \mathrm{d}^2 A \\[4pt] \texttt{(} A \texttt{)} & \mathrm{d}A & \mathrm{d}^2 A \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] {}^{\shortparallel} & {}^{\shortparallel} & {}^{\shortparallel} \end{matrix}\) |
Because the initial space \(X = \langle A \rangle\) is one-dimensional, we can easily fit the second order extension \(\mathrm{E}^2 X = \langle A, \mathrm{d}A, \mathrm{d}^2 A \rangle\) within the compass of a single venn diagram, charting the pair of converging trajectories as shown in Figure 12.
| \(\text{Figure 12. The Anchor}\) |
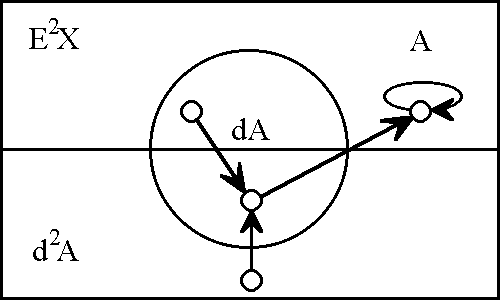
If we eliminate from view the regions of \(\mathrm{E}^2 X\) ruled out by the dynamic law \(\mathrm{d}^2 A = \texttt{(} A \texttt{)}\) then what remains is the quotient structure shown in Figure 13. The picture makes it easy to see how the dynamically allowable portion of the universe is partitioned between the respective holdings of \(A\) and \(\mathrm{d}^2 A.\) As it happens, the fact might have been expressed “right off the bat” by an equivalent formulation of the differential law, one which uses the exclusive disjunction to state the law as \(\texttt{(} A \texttt{,} \mathrm{d}^2 A \texttt{)}.\)
| \(\text{Figure 13. The Tiller}\) |
What we have achieved in this example is to give a differential description of a simple dynamic process. We did this by embedding a directed graph, representing the state transitions of a finite automaton, in the share of a boolean lattice or n‑cube cut out by nullifying all the regions the dynamics outlaws.
With growth in the dimensions of our contemplated universes it becomes essential, both for human comprehension and for computer implementation, that dynamic structures of interest be represented not actually, by acquaintance, but virtually, by description. In our present study we are using the language of propositional calculus to express the relevant descriptions, and to grasp the structures embodied in subsets of n‑cubes without being forced to actualize all their points.
Commentary On Small Models
One reason for engaging in our present order of extremely reduced but explicitly controlled case study is to throw light on the general study of languages, formal and natural, in their full array of syntactic, semantic, and pragmatic aspects. Propositional calculus is one of the last points of departure where it is possible to see that trio of aspects interacting in a non‑trivial way without being immediately and totally overwhelmed by the complexity they generate.
The generative complexity of formal and natural languages tends to lead investigators to adopt the strategy of focusing on a single aspect of the domain, abandoning hope of understanding the whole, whether it is the still living natural language or the dynamics of inquiry crystallized in formal logic.
In the perspective adopted here, a language is a syntactic system evolved or designed to express a set of descriptions. If the explicit symbols of a language have extensions in its object world which are actually infinite, or if the implicit categories and generative devices of a linguistic theory have extensions in its subject matter which are potentially infinite, then the finite characters of terms, statements, arguments, grammars, logics, and rhetorics force a surplus intension to color the symbols and functions of that language, all across the spectrum from object language to metalinguistic reflection.
In the aphorism of Wilhelm von Humboldt often cited by Chomsky, for example, in [Cho86, 30] and [Cho93, 49], language requires “the infinite use of finite means”. That is necessarily true when the extensions are infinite, when the referential symbols and grammatical categories of a language possess infinite sets of models and instances. But it also voices a practical truth when the extensions, though finite at every stage, tend to grow at exponential rates.
This consequence of dealing with extensions that are “practically infinite” becomes crucial when one tries to build neural network systems that learn, since the learning competence of any intelligent system is limited to the objects and domains that it is able to represent. If we want to design systems that operate intelligently with the full deck of propositions dealt by intact universes of discourse, then we must supply them with succinct representations and efficient transformations in this domain. Furthermore, in the project of constructing inquiry driven systems, we find ourselves forced to contemplate the level of generality that is embodied in propositions, because the dynamic evolution of these systems is driven by the measurable discrepancies that occur among their expectations, intentions, and observations, and because each of these subsystems or components of knowledge constitutes a propositional modality that can take on the fully generic character of an empirical summary or an axiomatic theory.
A compression scheme by any other name is a symbolic representation, and this is what the differential extension of propositional calculus, through all of its many universes of discourse, is intended to supply. Why is this particular program of mental calisthenics worth carrying out in general? By providing a uniform logical medium for describing dynamic systems we can make the task of understanding complex systems much easier, both in looking for invariant representations of individual cases and in finding points of comparison among diverse structures that would otherwise appear as isolated systems. All of this goes to facilitate the search for compact knowledge and to adapt what is learned from individual cases to the general realm.
Back to the Feature
|
I guess it must be the flag of my disposition, out of hopeful | |
| — Walt Whitman, Leaves of Grass, [Whi, 31] |
Let us assume the sense intended for differential features is well enough established in the intuition for now that we may continue with outlining the structure of the differential extension \([\mathrm{E}\mathcal{X}] = [A, \mathrm{d}A].\)
The extended alphabet \(\mathrm{E}\mathcal{X} = \{ x_1, \mathrm{d}x_1 \} = \{ A, \mathrm{d}A \}\) of cardinality \(2^n = 2\) generates the terms of description for the extended space \(\mathrm{E}X\) of cardinality \(2^{2n} = 4\) according to the following series of equations.
|
\(\begin{array}{lll} \mathrm{E}X & = & \langle A, \mathrm{d}A \rangle \\[4pt] & = & \{ \texttt{(} A \texttt{)}, A \} ~\times~ \{ \texttt{(} \mathrm{d}A \texttt{)}, \mathrm{d}A \} \\[4pt] & = & \{ \texttt{(} A \texttt{)(} \mathrm{d}A \texttt{)},~ \texttt{(} A \texttt{)} \mathrm{d}A,~ A \texttt{(} \mathrm{d}A \texttt{)},~ A ~ \mathrm{d}A \}. \end{array}\) |
The space \(\mathrm{E}X\) may be assigned the mnemonic type \(\mathbb{B} \times \mathbb{D},\) which is really no different than \(\mathbb{B} \times \mathbb{B} = \mathbb{B}^2.\) An individual element of \(\mathrm{E}X\) may be regarded as a disposition at a point or a situated direction, in effect, a singular mode of change occurring at a single point in the universe of discourse. In applications, the modality of the change may be interpreted in various ways, for example, as an expectation, an intention, or an observation with respect to the behavior of a system.
To complete the construction of the extended universe of discourse \(\mathrm{E}X^\bullet = [x_1, \mathrm{d}x_1] = [A, \mathrm{d}A]\) one must add the set of differential propositions \(\mathrm{E}X^\uparrow = \{ g : \mathrm{E}X \to \mathbb{B} \} \cong (\mathbb{B} \times \mathbb{D} \to \mathbb{B})\) to the set of dispositions in \(\mathrm{E}X.\) There are \(2^{2^{2n}} = 16\) propositions in \(\mathrm{E}X^\uparrow,\) as detailed in Table 14.
| \(\text{Table 14. Differential Propositions}\) |
| 600px |
Aside from changing the names of variables and shuffling the order of rows, this Table follows the format that was used previously for boolean functions of two variables. The rows are grouped to reflect natural similarity classes among the propositions. In a future discussion, those classes will be given additional explanation and motivation as the orbits of a certain transformation group acting on the set of 16 propositions. Notice that four of the propositions, in their logical expressions, resemble those given in the table for \(X^\uparrow.\) Thus the first set of propositions \(\{ f_i \}\) is automatically embedded in the present set \(\{ g_j \}\) and the corresponding inclusions are indicated at the far left margin of the Table.
Tacit Extensions
|
I would really like to have slipped imperceptibly into this lecture, as into all the others I shall be delivering, perhaps over the years ahead. |
||
| — Michel Foucault, The Discourse on Language, [Fou, 215] | ||
In viewing the previous Table of Differential Propositions it is important to notice the subtle distinction in type between a function \(f_i : X \to \mathbb{B}\) and its inclusion as a function \(g_j : \mathrm{E}X \to \mathbb{B},\) even though they share the same logical expression. Naturally, we want to maintain the logical equivalence of expressions representing the same proposition while appreciating the full diversity of a proposition's functional and typical representatives. Both perspectives, and all the levels of abstraction extending through them, have their reasons, as will develop in time.
Because this special circumstance points to a broader theme, it's a good idea to discuss it more generally. Whenever there arises a situation like that above, where one basis \(\mathcal{X}\) is a subset of another basis \(\mathcal{Y},\) we say any proposition \(f : \langle \mathcal{X} \rangle \to \mathbb{B}\) has a tacit extension to a proposition \(\boldsymbol\varepsilon f : \langle \mathcal{Y} \rangle \to \mathbb{B}\) and we say the space \((\langle \mathcal{X} \rangle \to \mathbb{B})\) has an automatic embedding within the space \((\langle \mathcal{Y} \rangle \to \mathbb{B}).\)
The tacit extension operator \(\boldsymbol\varepsilon\) is defined in such a way that \(\boldsymbol\varepsilon f\) puts the same constraint on the variables of \(\mathcal{X}\) within \(\mathcal{Y}\) as the proposition \(f\) initially put on \(\mathcal{X},\) while it puts no constraint on the variables of \(\mathcal{Y}\) beyond \(\mathcal{X},\) in effect, conjoining the two constraints.
Indexing the variables as \(\mathcal{X} = \{ x_1, \ldots, x_n \}\) and \(\mathcal{Y} = \{ x_1, \ldots, x_n, \ldots, x_{n+k} \}\) the tacit extension from \(\mathcal{X}\) to \(\mathcal{Y}\) may be expressed by the following equation.
| \(\boldsymbol\varepsilon f(x_1, \ldots, x_n, \ldots, x_{n+k}) ~=~ f(x_1, \ldots, x_n).\) |
On formal occasions, such as the present context of definition, the tacit extension from \(\mathcal{X}\) to \(\mathcal{Y}\) is explicitly symbolized by the operator \(\boldsymbol\varepsilon : (\langle \mathcal{X} \rangle \to \mathbb{B}) \to (\langle \mathcal{Y} \rangle \to \mathbb{B}),\) where the bases \(\mathcal{X}\) and \(\mathcal{Y}\) are set in context, but it's normally understood the \(\text{“} \boldsymbol\varepsilon \text{”}\) may be silent.
Returning to the Table of Differential Propositions, let's examine how the general concept of a tacit extension applies to the differential extension of a one‑dimensional universe of discourse, where \(\mathcal{X} = \{ A \}\) and \(\mathcal{Y} = \mathrm{E}\mathcal{X} = \{ A, \mathrm{d}A \}.\)
Each proposition \(f_i : X \to \mathbb{B}\) has a canonical expression \(e_i\) in the set \(\{ 0, \texttt{(} A \texttt{)}, A, 1 \}.\) The tacit extension \(\boldsymbol\varepsilon f_i : \mathrm{E}X \to \mathbb{B}\) may then be expressed as a logical conjunction of two factors, \(f_i = e_i \cdot \tau,\) where \(\tau\) is a logical tautology using all the variables of \(\mathcal{Y} - \mathcal{X}.\) The following Table shows how the tacit extensions \(\boldsymbol\varepsilon f_i\) of the propositions \(f_i\) may be expressed in terms of the extended basis \(\{ A, \mathrm{d}A \}.\)
| \(\text{Table 15. Tacit Extension of}~ [A] ~\text{to}~ [A, \mathrm{d}A]\) |
| 600px |
In its bearing on the singular propositions over a universe of discourse \(X\) the above analysis has an interesting interpretation. The tacit extension takes us from thinking about a particular state, like \(A\) or \(\texttt{(} A \texttt{)},\) to considering the collection of outcomes, the outgoing changes or the singular dispositions, springing or stemming from that state.
Example 2. Drives and Their Vicissitudes
|
I open my scuttle at night and see the far-sprinkled systems, | |
| — Walt Whitman, Leaves of Grass, [Whi, 81] |
Before we leave the one‑feature case let's look at a more substantial example, one which illustrates a general class of curves through the extended feature spaces and provides an opportunity to discuss important themes concerning their structure and dynamics.
As before let \(\mathcal{X} = \{ x_1 \} = \{ A \}.\) The discussion to follow considers a class of trajectories having the property that \(\mathrm{d}^k A = 0\) for all \(k\) greater than a fixed value \(m\) and indulges in the use of a picturesque vocabulary to describe salient classes of those curves.
Given the above finite order condition, there is a highest order non‑zero difference \(\mathrm{d}^m A\) exhibited at each point of any trajectory one may wish to consider. With respect to any point of the corresponding curve let us call that highest order differential feature \(\mathrm{d}^m A\) the drive at that point. Curves of constant drive \(\mathrm{d}^m A\) are then referred to as \(m^\text{th}\)‑gear curves.
- Scholium. The fact that a difference calculus can be developed for boolean functions is well known [Fuji], [Koh, § 8-4] and was probably familiar to Boole, who was an expert in difference equations before he turned to logic. And of course there is the strange but true story of how the Turin machines of the 1840s prefigured the Turing machines of the 1940s [Men, 225-297]. At the very outset of general purpose, mechanized computing we find that the motive power driving the Analytical Engine of Babbage, the kernel of an idea behind all of his wheels, was exactly his notion that difference operations, suitably trained, can serve as universal joints for any conceivable computation [M&M], [Mel, ch. 4].
Expressed in terms of drives and gears our next Example may be described as the family of \(4^\text{th}\)‑gear curves in the fourth extension \(\mathrm{E}^4 X\) \(=\) \(\langle A, ~\mathrm{d}A, ~\mathrm{d}^2\!A, ~\mathrm{d}^3\!A, ~\mathrm{d}^4\!A \rangle.\) Those are the trajectories generated subject to the dynamic law \(\mathrm{d}^4 A = 1,\) where it's understood all higher order differences are equal to \(0.\)
Since \(\mathrm{d}^4 A\) and all higher differences \(\mathrm{d}^k A\) are fixed, the state vectors vary only with respect to their projections as points of \(\mathrm{E}^3 X\) \(=\) \(\langle A, ~\mathrm{d}A, ~\mathrm{d}^2\!A, ~\mathrm{d}^3\!A \rangle.\) Thus there is just enough space in a planar venn diagram to plot all the orbits and to show how they partition the points of \(\mathrm{E}^3 X.\) It turns out there are exactly two possible orbits, of eight points each, as shown in Figure 16.
| File:Diff Log Dyn Sys • Figure 16 • A Couple of Fourth Gear Orbits.gif |
| \(\text{Figure 16. A Couple of Fourth Gear Orbits}\) |
With a little thought it is possible to devise a canonical indexing scheme for the states in differential logical systems. A scheme of that order allows for comparing changes of state in universes of discourse that weigh in on different scales of observation.
To that purpose, let us index the states \(q \in \mathrm{E}^m X\) with the dyadic rationals (or the binary fractions) in the half-open interval \([0, 2).\) Formally and canonically, a state \(q_r\) is indexed by a fraction \(r = \tfrac{s}{t}\) whose denominator is the power of two \(t = 2^m\) and whose numerator is a binary numeral formed from the coefficients of state in a manner to be described next.
The differential coefficients of the state \(q\) are just the values \(\mathrm{d}^k\!A(q)\) for \(k = 0 ~\text{to}~ m,\) where \(\mathrm{d}^0\!A\) is defined as being identical to \(A.\) To form the binary index \(d_0.d_1 \ldots d_m\) of the state \(q\) the coefficient \(\mathrm{d}^k\!A(q)\) is read off as the binary digit \(d_k\) associated with the place value \(2^{-k}.\) Expressed by way of algebraic formulas, the rational index \(r\) of the state \(q\) is given by the following equivalent formulations.
|
\(\begin{matrix} r(q) & = & \displaystyle\sum_k d_k \cdot 2^{-k} & = & \displaystyle\sum_k \text{d}^k A(q) \cdot 2^{-k} \\[8pt] = \\[8pt] \displaystyle\frac{s(q)}{t} & = & \displaystyle\frac{\sum_k d_k \cdot 2^{(m-k)}}{2^m} & = & \displaystyle\frac{\sum_k \text{d}^k A(q) \cdot 2^{(m-k)}}{2^m} \end{matrix}\) |
Applied to the example of \(4^\text{th}\)‑gear curves, the indexing scheme results in the data of Tables 17‑a and 17‑b, showing one period for each orbit.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
The states in each orbit are listed as ordered pairs \((p_i, q_j),\) where \(p_i\) may be read as a temporal parameter indicating the present time of the state and where \(j\) is the decimal equivalent of the binary numeral \(s.\)
Grasped more intuitively, the Tables show each state \(q_s\) with a subscript \(s\) equal to the numerator of its rational index, taking for granted the constant denominator of \(2^4 = 16.\) In that way the temporal succession of states can be reckoned by a parallel round‑up rule. Namely, if \((d_k, d_{k+1})\) is any pair of adjacent digits in the state index \(r\) then the value of \( d_k\) in the next state is \({d_k}^\prime = d_k + d_{k+1}.\)
• Overview • Part 1 • Part 2 • Part 3 • Part 4 • Part 5 • Appendices • References • Document History •
- Pages with broken file links
- Adaptive systems
- Artificial intelligence
- Boolean algebra
- Boolean functions
- Category theory
- Combinatorics
- Computation theory
- Cybernetics
- Differential logic
- Discrete systems
- Dynamical systems
- Formal languages
- Formal sciences
- Formal systems
- Functional logic
- Graph theory
- Group theory
- Logic
- Logical graphs
- Neural networks
- Peirce, Charles Sanders
- Semiotics
- Systems theory
- Visualization