User:Jon Awbrey/SEQUENCES

A061396

• A061396

Plain Wiki Table

Large Scale

\(\text{Table 1.} ~~ \text{Prime Factorizations, Riffs, and Rotes}\)

\(\text{Integer}\!\)	\(\text{Factorization}\!\)	\(\text{Notation}\!\)	\(\text{Riff Digraph}\!\)	\(\text{Rote Graph}\!\)	\(\text{Traversal}\!\)
\(1\!\)	\(1\!\)
\(2\!\)	\(\text{p}_1^1\!\)	\(\text{p}\!\)			\(((~))\)
\(3\!\)	\(\begin{array}{lll} \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 \end{array}\)	\(\text{p}_\text{p}\!\)			\((((~))(~))\)
\(4\!\)	\(\begin{array}{lll} \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} \end{array}\)	\(\text{p}^\text{p}\!\)			\(((((~))))\)
\(5\!\)	\(\begin{array}{lll} \text{p}_3^1 & = & \text{p}_{\text{p}_2^1}^1 \\[6pt] & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 \end{array}\)	\(\text{p}_{\text{p}_{\text{p}}}\!\)			\(((((~))(~))(~))\)
\(6\!\)	\(\begin{array}{lll} \text{p}_1^1 \text{p}_2^1 & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 \end{array}\)	\(\text{p} \text{p}_{\text{p}}\!\)			\(((~))(((~))(~))\)
\(7\!\)	\(\begin{array}{lll} \text{p}_4^1 & = & \text{p}_{\text{p}_1^2}^1 \\[6pt] & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 \end{array}\)	\(\text{p}_{\text{p}^{\text{p}}}\!\)			\((((((~))))(~))\)
\(8\!\)	\(\begin{array}{lll} \text{p}_1^3 & = & \text{p}_1^{\text{p}_2^1} \\[6pt] & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} \end{array}\)	\(\text{p}^{\text{p}_{\text{p}}}\!\)			\((((((~))(~))))\)
\(9\!\)	\(\begin{array}{lll} \text{p}_2^2 & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \end{array}\)	\(\text{p}_\text{p}^\text{p}\!\)			\((((~))(((~))))\)
\(16\!\)	\(\begin{array}{lll} \text{p}_1^4 & = & \text{p}_1^{\text{p}_1^2} \\[6pt] & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} \end{array}\)	\(\text{p}^{\text{p}^{\text{p}}}\!\)			\(((((((~))))))\)

Small Scale

\(\text{Table 1.} ~~ \text{Prime Factorizations, Riffs, and Rotes}\)

\(\text{Integer}\!\)	\(\text{Factorization}\!\)	\(\text{Notation}\!\)	\(\text{Riff Digraph}\!\)	\(\text{Rote Graph}\!\)	\(\text{Traversal}\!\)
\(1\!\)	\(1\!\)
\(2\!\)	\(\text{p}_1^1\!\)	\(\text{p}\!\)			\(((~))\)
\(3\!\)	\(\begin{array}{lll} \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 \end{array}\)	\(\text{p}_\text{p}\!\)			\((((~))(~))\)
\(4\!\)	\(\begin{array}{lll} \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} \end{array}\)	\(\text{p}^\text{p}\!\)			\(((((~))))\)
\(5\!\)	\(\begin{array}{lll} \text{p}_3^1 & = & \text{p}_{\text{p}_2^1}^1 \\[6pt] & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 \end{array}\)	\(\text{p}_{\text{p}_{\text{p}}}\!\)			\(((((~))(~))(~))\)
\(6\!\)	\(\begin{array}{lll} \text{p}_1^1 \text{p}_2^1 & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 \end{array}\)	\(\text{p} \text{p}_{\text{p}}\!\)			\(((~))(((~))(~))\)
\(7\!\)	\(\begin{array}{lll} \text{p}_4^1 & = & \text{p}_{\text{p}_1^2}^1 \\[6pt] & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 \end{array}\)	\(\text{p}_{\text{p}^{\text{p}}}\!\)			\((((((~))))(~))\)
\(8\!\)	\(\begin{array}{lll} \text{p}_1^3 & = & \text{p}_1^{\text{p}_2^1} \\[6pt] & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} \end{array}\)	\(\text{p}^{\text{p}_{\text{p}}}\!\)			\((((((~))(~))))\)
\(9\!\)	\(\begin{array}{lll} \text{p}_2^2 & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \end{array}\)	\(\text{p}_\text{p}^\text{p}\!\)			\((((~))(((~))))\)
\(16\!\)	\(\begin{array}{lll} \text{p}_1^4 & = & \text{p}_1^{\text{p}_1^2} \\[6pt] & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} \end{array}\)	\(\text{p}^{\text{p}^{\text{p}}}\!\)			\(((((((~))))))\)

Nested Wiki Table

Large Scale

\(\text{Table 1.} ~~ \text{Prime Factorizations, Riffs, and Rotes}\)

\(\text{Integer}\!\) \(\text{Factorization}\!\) \(\text{Notation}\!\) \(\text{Riff Digraph}\!\) \(\text{Rote Graph}\!\) \(\text{Traversal}\!\)

\(1\!\) \(1\!\)

\(2\!\) \(\text{p}_1^1\!\) \(\text{p}\!\) \(((~))\)

\(3\!\) \(\begin{array}{lll} \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p}_\text{p}\!\) \((((~))(~))\) \(4\!\) \(\begin{array}{lll} \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} \end{array}\) \(\text{p}^\text{p}\!\) \(((((~))))\)

\(5\!\) \(\begin{array}{lll} \text{p}_3^1 & = & \text{p}_{\text{p}_2^1}^1 \\[10pt] & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 \end{array}\) \(\text{p}_{\text{p}_{\text{p}}}\!\) \(((((~))(~))(~))\) \(6\!\) \(\begin{array}{lll} \text{p}_1^1 \text{p}_2^1 & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p} \text{p}_{\text{p}}\!\) \(((~))(((~))(~))\) \(7\!\) \(\begin{array}{lll} \text{p}_4^1 & = & \text{p}_{\text{p}_1^2}^1 \\[10pt] & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 \end{array}\) \(\text{p}_{\text{p}^{\text{p}}}\!\) \((((((~))))(~))\) \(8\!\) \(\begin{array}{lll} \text{p}_1^3 & = & \text{p}_1^{\text{p}_2^1} \\[10pt] & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} \end{array}\) \(\text{p}^{\text{p}_{\text{p}}}\!\) \((((((~))(~))))\) \(9\!\) \(\begin{array}{lll} \text{p}_2^2 & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \end{array}\) \(\text{p}_\text{p}^\text{p}\!\) \((((~))(((~))))\) \(16\!\) \(\begin{array}{lll} \text{p}_1^4 & = & \text{p}_1^{\text{p}_1^2} \\[10pt] & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} \end{array}\) \(\text{p}^{\text{p}^{\text{p}}}\!\) \(((((((~))))))\)

Small Scale

\(\text{Table 1.} ~~ \text{Prime Factorizations, Riffs, and Rotes}\)

\(\text{Integer}\!\) \(\text{Factorization}\!\) \(\text{Notation}\!\) \(\text{Riff Digraph}\!\) \(\text{Rote Graph}\!\) \(\text{Traversal}\!\)

\(1\!\) \(1\!\)

\(2\!\) \(\text{p}_1^1\!\) \(\text{p}\!\) \(((~))\)

\(3\!\) \(\begin{array}{lll} \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p}_\text{p}\!\) \((((~))(~))\) \(4\!\) \(\begin{array}{lll} \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} \end{array}\) \(\text{p}^\text{p}\!\) \(((((~))))\)

\(5\!\) \(\begin{array}{lll} \text{p}_3^1 & = & \text{p}_{\text{p}_2^1}^1 \\[10pt] & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 \end{array}\) \(\text{p}_{\text{p}_{\text{p}}}\!\) \(((((~))(~))(~))\) \(6\!\) \(\begin{array}{lll} \text{p}_1^1 \text{p}_2^1 & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p} \text{p}_{\text{p}}\!\) \(((~))(((~))(~))\) \(7\!\) \(\begin{array}{lll} \text{p}_4^1 & = & \text{p}_{\text{p}_1^2}^1 \\[10pt] & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 \end{array}\) \(\text{p}_{\text{p}^{\text{p}}}\!\) \((((((~))))(~))\) \(8\!\) \(\begin{array}{lll} \text{p}_1^3 & = & \text{p}_1^{\text{p}_2^1} \\[10pt] & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} \end{array}\) \(\text{p}^{\text{p}_{\text{p}}}\!\) \((((((~))(~))))\) \(9\!\) \(\begin{array}{lll} \text{p}_2^2 & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \end{array}\) \(\text{p}_\text{p}^\text{p}\!\) \((((~))(((~))))\) \(16\!\) \(\begin{array}{lll} \text{p}_1^4 & = & \text{p}_1^{\text{p}_1^2} \\[10pt] & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} \end{array}\) \(\text{p}^{\text{p}^{\text{p}}}\!\) \(((((((~))))))\)

Old ASCII Version

Illustration of initial terms of A061396
Jon Awbrey (jawbrey(AT)oakland.edu)

o--------------------------------------------------------------------------------
| integer   factorization     riff      r.i.f.f.     rote   -->   in parentheses
|                             k p's     k nodes      2k+1 nodes
o--------------------------------------------------------------------------------
|
| 1         1                 blank     blank        @            blank
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
| 2         p_1^1             p         @            @            (())
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
| 3         p_2^1 =                                  |
|           p_(p_1)^1         p_p       @            @            ((())())
|                                        ^
|                                         \
|                                          o
|
|                                                        o---o
|                                          o             |
|                                         ^          o---o
| 4         p_1^2 =                      /           |
|           p_1^p_1           p^p       @            @            (((())))
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
|                                                    |
| 5         p_3 =                                    o---o
|           p_(p_2) =                                |
|           p_(p_(p_1))       p_(p_p)   @            @            (((())())())
|                                        ^
|                                         \
|                                          o
|                                           ^
|                                            \
|                                             o
|
|                                                        o-o
|                                                       /
|                                                  o-o o-o
| 6         p_1 p_2 =                               \ /
|           p_1 p_(p_1)       p p_p     @ @          @            (())((())())
|                                          ^
|                                           \
|                                            o
|
|                                                        o---o
|                                                        |
|                                                    o---o
|                                                    |
| 7         p_4 =                                    o---o
|           p_(p_1^2) =                              |
|           p_(p_1^p_1)       p_(p^p)   @     o      @            ((((())))())
|                                        ^   ^
|                                         \ /
|                                          o
|
|                                                        o---o
|                                                        |
|                                                        o---o
|                                          o             |
| 8         p_1^3 =                       ^ ^        o---o
|           p_1^p_2 =                    /   \       |
|           p_1^p_(p_1)       p^p_p     @     o      @            ((((())())))
|
|                                                    o-o o-o
|                                          o         |   |
| 9         p_2^2 =                       ^          o---o
|           p_(p_1)^2 =                  /           |
|           p_(p_1)^(p_1)     p_p^p     @            @            ((())((())))
|                                        ^
|                                         \
|                                          o
|
|                                             o              o---o
|                                            ^               |
|                                           /            o---o
|                                          o             |
| 16        p_1^4 =                       ^          o---o
|           p_1^(p_1^2) =                /           |
|           p_1^(p_1^p_1)     p^(p^p)   @            @            (((((())))))
|
o--------------------------------------------------------------------------------

Further Comments:

Here are a couple more pages from my notes,
where it looks like I first arrived at the
generating function, and also carried out
some brute force enumerations of riffs.

I am going to experiment with a different way of
transcribing indices and powers into a plaintext.

|                jj
|              p<
|      j      /  ji
|    p<     p<         etc.
|      i      \  ij
|              p<
|                ii

-------------------------------------------------------

1978-11-06

Generating Function

| R(x) = 1 + x + 2x^2 + ...
|
|      =   1 + x.x^0 (1 + x + 2x^2 + ...)
|        . 1 + x.x^1 (1 + x + 2x^2 + ...)
|        . 1 + x.x^2 (1 + x + 2x^2 + ...)
|        . 1 + x.x^2 (1 + x + 2x^2 + ...)
|        . ...
|
|      = 1 + x + 2x^2 + ...
|
| Product over (i = 0 to infinity) of (1 + x.x^i.R(x))^R_i  =  R(x)

-------------------------------------------------------

1978-11-10

Brute force enumeration of R_n

| 4 p's
|
|       p
|     p<        p_p                 p                    p
|   p<        p<        p p_p     p<_p     p_p_p     p_p<
| p<        p<        p<        p<       p<        p<
|
|
|       p
|     p<        p_p                 p                    p
| p_p<      p_p<      p<        p_p<_p   p_p_p_p   p_p_p<
|                       p p_p
|
|
|     p
|   p<        p_p       p         p        p           p
| p<        p<        p<        p<       p<  p<    p p<
|   p         p         p_p       p^p          p       p
|
|
| p p_p_p   p p<
|               p^p
|

Altogether, 20 riffs of weight 4.

| o---------------------o---------------------o---------------------o
| | 3                   | 4                   | 5                   |
| o---------------------o---------------------o---------------------|
| | // // 2             | 10, 3, 1, 6         | 36, 10, 2, 3, 2, 20 |
| o---------------------o---------------------o---------------------|
| |                     | 0^1 4^1,            |                     |
| |                     | 1^1 3^1,            |                     |
| |                     | 2^2,                |                     |
| |                     | 4^1 0^1             |                     |
| o---------------------o---------------------o---------------------o
| | 6                   | 20                  | 73                  |
| o---------------------o---------------------o---------------------o
|

-------------------------------------------------------

Here are the number values of the riffs on 4 nodes:

o----------------------------------------------------------------------
|
|       p
|     p<        p_p                 p                    p
|   p<        p<        p p_p     p<_p     p_p_p     p_p<
| p<        p<        p<        p<       p<        p<
|
| 2^16      2^8       2^6       2^9      2^5       2^7
| 65536     256       64        512      32        128
o----------------------------------------------------------------------
|
|       p
|     p<        p_p                 p                    p
| p_p<      p_p<      p<        p_p<_p   p_p_p_p   p_p_p<
|                       p p_p
|
| p_16      p_8       p_6       p_9      p_5       p_7
| 53        19        13        23       11        17
o----------------------------------------------------------------------
|
|     p
|   p<        p_p       p         p                    p
| p<        p<        p<        p<       p^p p_p   p p<
|   p         p         p_p       p^p                  p
|
| 3^4       3^3       5^2       7^2
| 81        27        25        49       12        18
o----------------------------------------------------------------------
|
| p p_p_p   p p<
|               p^p
|
| 10        14 
o----------------------------------------------------------------------

For ease of reference, I include the previous table
of smaller riffs and rotes, redone in the new style.

o--------------------------------------------------------------------------------
| integer   factorization     riff      r.i.f.f.     rote   -->   in parentheses
|                             k p's     k nodes      2k+1 nodes
o--------------------------------------------------------------------------------
|
| 1         1                 blank     blank        @            blank
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
| 2         p_1^1             p         @            @            (())
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
| 3         p_2^1 =                                  |
|           p_(p_1)^1         p_p       @            @            ((())())
|                                        ^
|                                         \
|                                          o
|
|                                                        o---o
|                                          o             |
|                                         ^          o---o
| 4         p_1^2 =                      /           |
|           p_1^p_1           p^p       @            @            (((())))
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
|                                                    |
| 5         p_3 =                                    o---o
|           p_(p_2) =                                |
|           p_(p_(p_1))       p_p_p     @            @            (((())())())
|                                        ^
|                                         \
|                                          o
|                                           ^
|                                            \
|                                             o
|
|                                                        o-o
|                                                       /
|                                                  o-o o-o
| 6         p_1 p_2 =                               \ /
|           p_1 p_(p_1)       p p_p     @ @          @            (())((())())
|                                          ^
|                                           \
|                                            o
|
|                                                        o---o
|                                                        |
|                                                    o---o
|                                                    |
| 7         p_4 =                                    o---o
|           p_(p_1^2) =                              |
|           p_(p_1^p_1)       p<        @     o      @            ((((())))())
|                               p^p      ^   ^
|                                         \ /
|                                          o
|
|                                                        o---o
|                                                        |
|                                                        o---o
|                                          o             |
| 8         p_1^3 =                       ^ ^        o---o
|           p_1^p_2 =           p_p      /   \       |
|           p_1^p_(p_1)       p<        @     o      @            ((((())())))
|
|                                                    o-o o-o
|                                          o         |   |
| 9         p_2^2 =                       ^          o---o
|           p_(p_1)^2 =         p        /           |
|           p_(p_1)^(p_1)     p<        @            @            ((())((())))
|                               p        ^
|                                         \
|                                          o
|
|                                             o              o---o
|                                            ^               |
|                                           /            o---o
|                                          o             |
| 16        p_1^4 =               p       ^          o---o
|           p_1^(p_1^2) =       p<       /           |
|           p_1^(p_1^p_1)     p<        @            @            (((((())))))
|
o--------------------------------------------------------------------------------

(later)

Expanded version of first table:

o--------------------------------------------------------------------------------
| integer   factorization     riff      r.i.f.f.     rote   -->   in parentheses
|                             k p's     k nodes      2k+1 nodes
o--------------------------------------------------------------------------------
|
| 1         1                 blank     blank        @            blank
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
| 2         p_1^1             p         @            @            (())
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
| 3         p_2^1 =                                  |
|           p_(p_1)^1         p_p       @            @            ((())())
|                                        ^
|                                         \
|                                          o
|
|                                                        o---o
|                                          o             |
|                                         ^          o---o
| 4         p_1^2 =                      /           |
|           p_1^p_1           p^p       @            @            (((())))
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
|                                                    |
| 5         p_3 =                                    o---o
|           p_(p_2) =                                |
|           p_(p_(p_1))       p_p_p     @            @            (((())())())
|                                        ^
|                                         \
|                                          o
|                                           ^
|                                            \
|                                             o
|
|                                                        o-o
|                                                       /
|                                                  o-o o-o
| 6         p_1 p_2 =                               \ /
|           p_1 p_(p_1)       p p_p     @ @          @            (())((())())
|                                          ^
|                                           \
|                                            o
|
|                                                        o---o
|                                                        |
|                                                    o---o
|                                                    |
| 7         p_4 =                                    o---o
|           p_(p_1^2) =                              |
|           p_(p_1^p_1)       p<        @     o      @            ((((())))())
|                               p^p      ^   ^
|                                         \ /
|                                          o
|
|                                                        o---o
|                                                        |
|                                                        o---o
|                                          o             |
| 8         p_1^3 =                       ^ ^        o---o
|           p_1^p_2 =           p_p      /   \       |
|           p_1^p_(p_1)       p<        @     o      @            ((((())())))
|
|                                                    o-o o-o
|                                          o         |   |
| 9         p_2^2 =                       ^          o---o
|           p_(p_1)^2 =         p        /           |
|           p_(p_1)^(p_1)     p<        @            @            ((())((())))
|                               p        ^
|                                         \
|                                          o
|
|                                             o              o---o
|                                            ^               |
|                                           /            o---o
|                                          o             |
| 16        p_1^4 =               p       ^          o---o
|           p_1^(p_1^2) =       p<       /           |
|           p_1^(p_1^p_1)     p<        @            @            (((((())))))
|
o--------------------------------------------------------------------------------

o================================================================================
|
|       p
|     p<        p          p_p         p
|   p<        p<_p       p<        p_p<      p p_p     p_p_p
| p<        p<         p<        p<        p<        p<
|
| 2^16      2^9        2^8       2^7       2^6       2^5
| 65536     512        256       128       64        32
|
o--------------------------------------------------------------------------------
|
|       p
|     p<        p          p_p         p
| p_p<      p_p<_p     p_p<      p_p_p<    p<        p_p_p_p
|                                            p p_p
|
| p_16      p_9        p_8       p_7       p_6       p_5
| 53        23         19        17        13        11
|
o--------------------------------------------------------------------------------
|
|   p^p       p_p        p         p
| p<        p<         p<        p<
|   p         p          p^p       p_p
|
| 3^4       3^3        7^2       5^2
| 81        27         49        25
|
o--------------------------------------------------------------------------------
|
|     p
| p p<      p p<       p^p p_p   p p_p_p
|     p         p^p
|
| 18        14         12        10
|
o================================================================================

Triangle in which k-th row lists natural number
values for the collection of riffs with k nodes.

k | natural numbers n such that |riff(n)| = k
--o------------------------------------------------
0 | 1;
1 | 2;
2 | 3, 4;
3 | 5, 6, 7, 8, 9, 16;
4 | 10, 11, 12, 13, 14, 17, 18, 19, 23, 25, 27,
  | 32, 49, 53, 64, 81, 128, 256, 512, 65536;

The natural number values for the riffs with
at most 3 pts are as follows (@'s are roots):

|                  o       o  o       o
|                  |       ^  |       ^
|                  v       |  v       |
|            o  o  o    o  o  o  o o  o
|            |  ^  |    |  |  ^  | ^  ^
|            v  |  v    v  v  |  v/   |
| Riff:   @; @, @; @, @ @, @, @, @,   @;
|
| Value:  2; 3, 4; 5,  6 , 7, 8, 9,  16;

---------------------------------------------------

1, 2, 3, 4, 5, 6, 7, 8, 9, 16,
10, 11, 12, 13, 14, 17, 18, 19,
23, 25, 27, 32, 49, 53, 64, 81,
128, 256, 512, 65536,

---------------------------------------------------

1; 2; 3, 4; 5, 6, 7, 8, 9, 16;
10, 11, 12, 13, 14, 17, 18, 19,
23, 25, 27, 32, 49, 53, 64, 81,
128, 256, 512, 65536;

---------------------------------------------------

A062504

• A062504

TeX Array

\(\begin{array}{l|l|r} k & P_k = \{ n : \operatorname{riff}(n) ~\text{has}~ k ~\text{nodes} \} = \{ n : \operatorname{rote}(n) ~\text{has}~ 2k + 1 ~\text{nodes} \} & |P_k| \\[10pt] 0 & \{ 1 \} & 1 \\ 1 & \{ 2 \} & 1 \\ 2 & \{ 3, 4 \} & 2 \\ 3 & \{ 5, 6, 7, 8, 9, 16 \} & 6 \\ 4 & \{ 10, 11, 12, 13, 14, 17, 18, 19, 23, 25, 27, 32, 49, 53, 64, 81, 128, 256, 512, 65536 \} & 20 \end{array}\)

JPEG

\(\text{Prime Factorizations, Riffs, and Rotes}\!\)

\(\text{Integer}\!\) \(\text{Factorization}\!\) \(\text{Notation}\!\) \(\text{Riff Digraph}\!\) \(\text{Rote Graph}\!\)

\(1\!\) \(1\!\)

\(2\!\) \(\text{p}_1^1\!\) \(\text{p}\!\)

\(3\!\) \(\begin{array}{lll} \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p}_\text{p}\!\) \(4\!\) \(\begin{array}{lll} \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} \end{array}\) \(\text{p}^\text{p}\!\)

\(5\!\) \(\begin{array}{lll} \text{p}_3^1 & = & \text{p}_{\text{p}_2^1}^1 \\[10pt] & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 \end{array}\) \(\text{p}_{\text{p}_{\text{p}}}\!\) \(6\!\) \(\begin{array}{lll} \text{p}_1^1 \text{p}_2^1 & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p} \text{p}_{\text{p}}\!\) \(7\!\) \(\begin{array}{lll} \text{p}_4^1 & = & \text{p}_{\text{p}_1^2}^1 \\[10pt] & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 \end{array}\) \(\text{p}_{\text{p}^{\text{p}}}\!\) \(8\!\) \(\begin{array}{lll} \text{p}_1^3 & = & \text{p}_1^{\text{p}_2^1} \\[10pt] & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} \end{array}\) \(\text{p}^{\text{p}_{\text{p}}}\!\) \(9\!\) \(\begin{array}{lll} \text{p}_2^2 & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \end{array}\) \(\text{p}_\text{p}^\text{p}\!\) \(16\!\) \(\begin{array}{lll} \text{p}_1^4 & = & \text{p}_1^{\text{p}_1^2} \\[10pt] & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} \end{array}\) \(\text{p}^{\text{p}^{\text{p}}}\!\)

ASCII

 Example

    * k | natural numbers n such that |riff(n)| = k
    * 0 | 1;
    * 1 | 2;
    * 2 | 3, 4;
    * 3 | 5, 6, 7, 8, 9, 16;
    * 4 | 10, 11, 12, 13, 14, 17, 18, 19, 23, 25, 27, 32, 49, 53, 64, 81, 128, 256, 512, 65536;
    * The natural number values for the riffs with at most 3 pts are as follows (x = root):
    * .................o.......o..o.......o
    * .................|.......^..|.......^
    * .................v.......|..v.......|
    * ...........o..o..o....o..o..o..o.o..o
    * ...........|..^..|....|..|..^..|.^..^
    * ...........v..|..v....v..v..|..v/...|
    * Riff:...x;.x,.x;.x,.x.x,.x,.x,.x,...x;
    * Value:..2;.3,.4;.5,..6.,.7,.8,.9,..16; 

A062537

• A062537

Wiki + TeX + JPEG

\(a(n) = \text{Number of Nodes in the Riff of}~ n\)

\(a(1) ~=~ 0\)	\(\text{p}\!\) \(a(2) ~=~ 1\)	\(\text{p}_\text{p}\!\) \(a(3) ~=~ 2\)	\(\text{p}^\text{p}\!\) \(a(4) ~=~ 2\)	\(\text{p}_{\text{p}_{\text{p}}}\!\) \(a(5) ~=~ 3\)
\(\text{p} \text{p}_{\text{p}}\!\) \(a(6) ~=~ 3\)	\(\text{p}_{\text{p}^{\text{p}}}\!\) \(a(7) ~=~ 3\)	\(\text{p}^{\text{p}_{\text{p}}}\!\) \(a(8) ~=~ 3\)	\(\text{p}_\text{p}^\text{p}\!\) \(a(9) ~=~ 3\)	\(\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(10) ~=~ 4\)
\(\text{p}_{\text{p}_{\text{p}_{\text{p}}}}\!\) \(a(11) ~=~ 4\)	\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(a(12) ~=~ 4\)	\(\text{p}_{\text{p} \text{p}_{\text{p}}}\!\) \(a(13) ~=~ 4\)	\(\text{p} \text{p}_{\text{p}^{\text{p}}}\!\) \(a(14) ~=~ 4\)	\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(15) ~=~ 5\)
\(\text{p}^{\text{p}^{\text{p}}}\!\) \(a(16) ~=~ 3\)	\(\text{p}_{\text{p}_{\text{p}^{\text{p}}}}\!\) \(a(17) ~=~ 4\)	\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(18) ~=~ 4\)	\(\text{p}_{\text{p}^{\text{p}_{\text{p}}}}\!\) \(a(19) ~=~ 4\)	\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(20) ~=~ 5\)
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(21) ~=~ 5\)	\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(22) ~=~ 5\)	\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(23) ~=~ 4\)	\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(a(24) ~=~ 5\)	\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(25) ~=~ 4\)
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(26) ~=~ 5\)	\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(27) ~=~ 4\)	\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(28) ~=~ 5\)	\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(29) ~=~ 5\)	\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(30) ~=~ 6\)

A062860

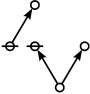
• A062860

Wiki + TeX + JPEG

\(a(n) = \text{Least Integer}~ j ~\text{with}~ n ~\text{Nodes in Its Riff}\)

\(1\!\) \(a(0) ~=~ 1\)

\(\text{p}\!\) \(a(1) ~=~ 2\)

\(\text{p}_\text{p}\!\) \(a(2) ~=~ 3\)

\(\text{p}_{\text{p}_{\text{p}}}\!\) \(a(3) ~=~ 5\)

\(\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(4) ~=~ 10\)

\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}}}\!\) \(a(5) ~=~ 15\)

\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(6) ~=~ 30\)

A106177

• A106177

Primal Codes of Finite Partial Functions on Positive Integers

\(\begin{array}{rcl} 1 & = & \varnothing \\ 2 & = & 1\!:\!1 \\ 3 & = & 2\!:\!1 \\ 4 & = & 1\!:\!2 \\ 5 & = & 3\!:\!1 \\ 6 & = & 1\!:\!1 ~~ 2\!:\!1 \\ 7 & = & 4\!:\!1 \\ 8 & = & 1\!:\!3 \\ 9 & = & 2\!:\!2 \\ 10 & = & 1\!:\!1 ~~ 3\!:\!1 \\ 11 & = & 5\!:\!1 \\ 12 & = & 1\!:\!2 ~~ 2\!:\!1 \\ 13 & = & 6\!:\!1 \\ 14 & = & 1\!:\!1 ~~ 4\!:\!1 \\ 15 & = & 2\!:\!1 ~~ 3\!:\!1 \\ 16 & = & 1\!:\!4 \\ 17 & = & 7\!:\!1 \\ 18 & = & 1\!:\!1 ~~ 2\!:\!2 \\ 19 & = & 8\!:\!1 \\ 20 & = & 1\!:\!2 ~~ 3\!:\!1 \end{array}\)

Wiki Table

									1		1
								2		1		2
							3		1		1		3
						4		1		2		1		4
					5		1		3		1		1		5
				6		1		1		1		4		1		6
			7		1		5		2		9		1		1		7
		8		1		6		1		1		1		2		1		8
	9		1		7		1		25		1		3		1		1		9
10		1		1		1		36		1		2		1		8		1		10

Wiki + TeX

Smallmatrix

\(\begin{smallmatrix} & & & & & & & & & {\color{red}1} & & {\color{red}1} \\ & & & & & & & & {\color{red}2} & & 1 & & {\color{red}2} \\ & & & & & & & {\color{red}3} & & 1 & & 1 & & {\color{red}3} \\ & & & & & & {\color{red}4} & & 1 & & 2 & & 1 & & {\color{red}4} \\ & & & & & {\color{red}5} & & 1 & & 3 & & 1 & & 1 & & {\color{red}5} \\ & & & & {\color{red}6} & & 1 & & 1 & & 1 & & 4 & & 1 & & {\color{red}6} \\ & & & {\color{red}7} & & 1 & & 5 & & 2 & & 9 & & 1 & & 1 & & {\color{red}7} \\ & & {\color{red}8} & & 1 & & 6 & & 1 & & 1 & & 1 & & 2 & & 1 & & {\color{red}8} \\ & {\color{red}9} & & 1 & & 7 & & 1 & & 25 & & 1 & & 3 & & 1 & & 1 & & {\color{red}9} \\ {\color{red}10} & & 1 & & 1 & & 1 & & 36 & & 1 & & 2 & & 1 & & 8 & & 1 & & {\color{red}10} \end{smallmatrix}\)

Array

\(\begin{array}{*{21}{c}} & & & & & & & & & {\color{red}1} & & {\color{red}1} \\ & & & & & & & & {\color{red}2} & & 1 & & {\color{red}2} \\ & & & & & & & {\color{red}3} & & 1 & & 1 & & {\color{red}3} \\ & & & & & & {\color{red}4} & & 1 & & 2 & & 1 & & {\color{red}4} \\ & & & & & {\color{red}5} & & 1 & & 3 & & 1 & & 1 & & {\color{red}5} \\ & & & & {\color{red}6} & & 1 & & 1 & & 1 & & 4 & & 1 & & {\color{red}6} \\ & & & {\color{red}7} & & 1 & & 5 & & 2 & & 9 & & 1 & & 1 & & {\color{red}7} \\ & & {\color{red}8} & & 1 & & 6 & & 1 & & 1 & & 1 & & 2 & & 1 & & {\color{red}8} \\ & {\color{red}9} & & 1 & & 7 & & 1 & & 25 & & 1 & & 3 & & 1 & & 1 & & {\color{red}9} \\ {\color{red}10} & & 1 & & 1 & & 1 & & 36 & & 1 & & 2 & & 1 & & 8 & & 1 & & {\color{red}10} \end{array}\)

Matrix

\(\begin{matrix} n \circ m \\ 1 ~/~\backslash~ 1 \\ 2 ~/~ 1 ~\backslash~ 2 \\ 3 ~/~ 1 \cdot 1 ~\backslash~ 3 \\ 4 ~/~ 1 \cdot 2 \cdot 1 ~\backslash~ 4 \\ 5 ~/~ 1 \cdot 3 \cdot 1 \cdot 1 ~\backslash~ 5 \\ 6 ~/~ 1 \cdot 1 \cdot 1 \cdot 4 \cdot 1 ~\backslash~ 6 \\ 7 ~/~ 1 \cdot 5 \cdot 2 \cdot 9 \cdot 1 \cdot 1 ~\backslash~ 7 \\ 8 ~/~ 1 \cdot 6 \cdot 1 \cdot 1 \cdot 1 \cdot 2 \cdot 1 ~\backslash~ 8 \\ 9 ~/~ 1 \cdot 7 \cdot 1 \cdot 25\cdot 1 \cdot 3 \cdot 1 \cdot 1 ~\backslash~ 9 \\ 10 ~/~ 1 \cdot 1 \cdot 1 \cdot 36\cdot 1 \cdot 2 \cdot 1 \cdot 8 \cdot 1 ~\backslash~ 10 \end{matrix}\)

ASCII

 Example

    *                      n o m
    *                       \ /
    *                      1 . 1
    *                     \ / \ /
    *                    2 . 1 . 2
    *                   \ / \ / \ /
    *                  3 . 1 . 1 . 3
    *                 \ / \ / \ / \ /
    *                4 . 1 . 2 . 1 . 4
    *               \ / \ / \ / \ / \ /
    *              5 . 1 . 3 . 1 . 1 . 5
    *             \ / \ / \ / \ / \ / \ /
    *            6 . 1 . 1 . 1 . 4 . 1 . 6
    *           \ / \ / \ / \ / \ / \ / \ /
    *          7 . 1 . 5 . 2 . 9 . 1 . 1 . 7
    *         \ / \ / \ / \ / \ / \ / \ / \ /
    *        8 . 1 . 6 . 1 . 1 . 1 . 2 . 1 . 8
    *       \ / \ / \ / \ / \ / \ / \ / \ / \ /
    *      9 . 1 . 7 . 1 . 25. 1 . 3 . 1 . 1 . 9
    *     \ / \ / \ / \ / \ / \ / \ / \ / \ / \ /
    *   10 . 1 . 1 . 1 . 36. 1 . 2 . 1 . 8 . 1 . 10
    *
    * Primal codes of finite partial functions on positive integers:
    * 1 = { }
    * 2 = 1:1
    * 3 = 2:1
    * 4 = 1:2
    * 5 = 3:1
    * 6 = 1:1 2:1
    * 7 = 4:1
    * 8 = 1:3
    * 9 = 2:2
    * 10 = 1:1 3:1
    * 11 = 5:1
    * 12 = 1:2 2:1
    * 13 = 6:1
    * 14 = 1:1 4:1
    * 15 = 2:1 3:1
    * 16 = 1:4
    * 17 = 7:1
    * 18 = 1:1 2:2
    * 19 = 8:1
    * 20 = 1:2 3:1

A109300

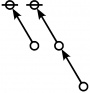
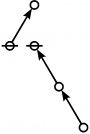
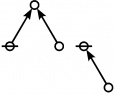
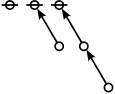
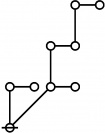
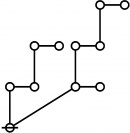
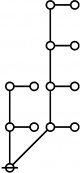
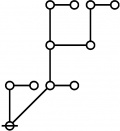
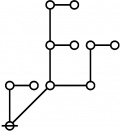
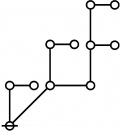
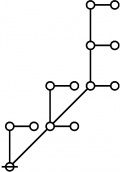
• A109300

JPEG

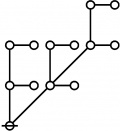
\(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\)

\(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\)

\(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}\)

\(\begin{array}{l} 2\!:\!2 \\ 9 \end{array}\)

\(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}\)

\(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}\)

\(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}\)

ASCII

 Example

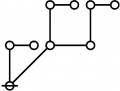
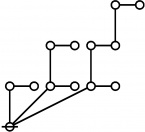
    * Table of Rotes and Primal Functions for Positive Integers of Rote Height 2
    *                                                                          
    * o-o     o-o       o-o   o-o o-o     o-o o-o       o-o o-o     o-o o-o o-o
    * |       |         |     |   |       |   |         |   |       |   |   |  
    * o-o   o-o     o-o o-o   o---o     o-o   o-o   o-o o---o     o-o   o---o  
    * |     |       |   |     |         |     |     |   |         |     |      
    * O     O       O===O     O         O=====O     O===O         O=====O      
    *                                                                          
    * 2:1   1:2     1:1 2:1   2:2       1:2 2:1     1:1 2:2       1:2 2:2      
    *                                                                          
    * 3     4       6         9         12          18            36           
    *                                                                           

A109301

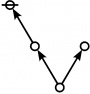
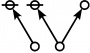
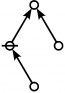
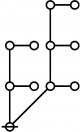
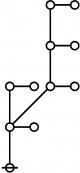
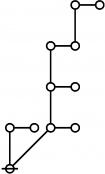
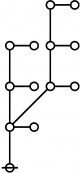
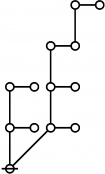
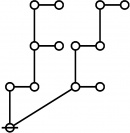
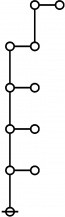
• A109301

JPEG

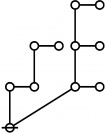
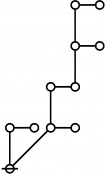
\(\begin{array}{l} \varnothing \\ 1 \end{array}\)	\(\begin{array}{l} 1\!:\!1 \\ 2 \end{array}\)	\(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\)	\(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\)	\(\begin{array}{l} 3\!:\!1 \\ 5 \end{array}\)
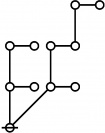
\(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 \\ 6 \end{array}\)	\(\begin{array}{l} 4\!:\!1 \\ 7 \end{array}\)	\(\begin{array}{l} 1\!:\!3 \\ 8 \end{array}\)	\(\begin{array}{l} 2\!:\!2 \\ 9 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!1 \\ 10 \end{array}\)
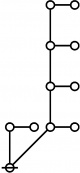
\(\begin{array}{l} 5\!:\!1 \\ 11 \end{array}\)	\(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 \\ 12 \end{array}\)	\(\begin{array}{l} 6\!:\!1 \\ 13 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 4\!:\!1 \\ 14 \end{array}\)	\(\begin{array}{l} 2\!:\!1 ~~ 3\!:\!1 \\ 15 \end{array}\)
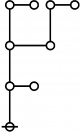
\(\begin{array}{l} 1\!:\!4 \\ 16 \end{array}\)	\(\begin{array}{l} 7\!:\!1 \\ 17 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!2 \\ 18 \end{array}\)	\(\begin{array}{l} 8\!:\!1 \\ 19 \end{array}\)	\(\begin{array}{l} 1\!:\!2 ~~ 3\!:\!1 \\ 20 \end{array}\)
\(\begin{array}{l} 2\!:\!1 ~~ 4\!:\!1 \\ 21 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 5\!:\!1 \\ 22 \end{array}\)	\(\begin{array}{l} 9\!:\!1 \\ 23 \end{array}\)	\(\begin{array}{l} 1\!:\!3 ~~ 2\!:\!1 \\ 24 \end{array}\)	\(\begin{array}{l} 3\!:\!2 \\ 25 \end{array}\)
\(\begin{array}{l} 1\!:\!1 ~~ 6\!:\!1 \\ 26 \end{array}\)	\(\begin{array}{l} 2\!:\!3 \\ 27 \end{array}\)	\(\begin{array}{l} 1\!:\!2 ~~ 4\!:\!1 \\ 28 \end{array}\)	\(\begin{array}{l} 10\!:\!1 \\ 29 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 30 \end{array}\)
\(\begin{array}{l} 11\!:\!1 \\ 31 \end{array}\)	\(\begin{array}{l} 1\!:\!5 \\ 32 \end{array}\)	\(\begin{array}{l} 2\!:\!1 ~~ 5\!:\!1 \\ 33 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 7\!:\!1 \\ 34 \end{array}\)	\(\begin{array}{l} 3\!:\!1 ~~ 4\!:\!1 \\ 35 \end{array}\)
\(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!2 \\ 36 \end{array}\)	\(\begin{array}{l} 12\!:\!1 \\ 37 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 8\!:\!1 \\ 38 \end{array}\)	\(\begin{array}{l} 2\!:\!1 ~~ 6\!:\!1 \\ 39 \end{array}\)	\(\begin{array}{l} 1\!:\!3 ~~ 3\!:\!1 \\ 40 \end{array}\)
\(\begin{array}{l} 13\!:\!1 \\ 41 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!1 ~~ 4\!:\!1 \\ 42 \end{array}\)	\(\begin{array}{l} 14\!:\!1 \\ 43 \end{array}\)	\(\begin{array}{l} 1\!:\!2 ~~ 5\!:\!1 \\ 44 \end{array}\)	\(\begin{array}{l} 2\!:\!2 ~~ 3\!:\!1 \\ 45 \end{array}\)
\(\begin{array}{l} 1\!:\!1 ~~ 9\!:\!1 \\ 46 \end{array}\)	\(\begin{array}{l} 15\!:\!1 \\ 47 \end{array}\)	\(\begin{array}{l} 1\!:\!4 ~~ 2\!:\!1 \\ 48 \end{array}\)	\(\begin{array}{l} 4\!:\!2 \\ 49 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 3\!:\!2 \\ 50 \end{array}\)
\(\begin{array}{l} 2\!:\!1 ~~ 7\!:\!1 \\ 51 \end{array}\)	\(\begin{array}{l} 1\!:\!2 ~~ 6\!:\!1 \\ 52 \end{array}\)	\(\begin{array}{l} 16\!:\!1 \\ 53 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 2\!:\!3 \\ 54 \end{array}\)	\(\begin{array}{l} 3\!:\!1 ~~ 5\!:\!1 \\ 55 \end{array}\)
\(\begin{array}{l} 1\!:\!3 ~~ 4\!:\!1 \\ 56 \end{array}\)	\(\begin{array}{l} 2\!:\!1 ~~ 8\!:\!1 \\ 57 \end{array}\)	\(\begin{array}{l} 1\!:\!1 ~~ 10\!:\!1 \\ 58 \end{array}\)	\(\begin{array}{l} 17\!:\!1 \\ 59 \end{array}\)	\(\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}\)

ASCII

 Comment

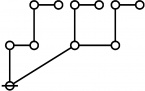
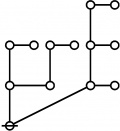
    * Table of Rotes and Primal Functions for Positive Integers from 1 to 40
    *                                                                        
    *                                                         o-o            
    *                                                         |              
    *                             o-o             o-o         o-o            
    *                             |               |           |              
    *               o-o           o-o           o-o           o-o            
    *               |             |             |             |              
    * O             O             O             O             O              
    *                                                                        
    * { }           1:1           2:1           1:2           3:1            
    *                                                                        
    * 1             2             3             4             5              
    *                                                                        
    *                                                                        
    *                 o-o           o-o                           o-o        
    *                 |             |                             |          
    *     o-o       o-o             o-o         o-o o-o           o-o        
    *     |         |               |           |   |             |          
    * o-o o-o       o-o           o-o           o---o         o-o o-o        
    * |   |         |             |             |             |   |          
    * O===O         O             O             O             O===O          
    *                                                                        
    * 1:1 2:1       4:1           1:3           2:2           1:1 3:1        
    *                                                                        
    * 6             7             8             9             10             
    *                                                                        
    *                                                                        
    * o-o                                                                    
    * |                                                                      
    * o-o                             o-o             o-o         o-o        
    * |                               |               |           |          
    * o-o             o-o o-o     o-o o-o           o-o       o-o o-o        
    * |               |   |       |   |             |         |   |          
    * o-o           o-o   o-o     o===o-o       o-o o-o       o-o o-o        
    * |             |     |       |             |   |         |   |          
    * O             O=====O       O             O===O         O===O          
    *                                                                        
    * 5:1           1:2 2:1       6:1           1:1 4:1       2:1 3:1        
    *                                                                        
    * 11            12            13            14            15             
    *                                                                        
    *                                                                        
    *                 o-o                         o-o                        
    *                 |                           |                          
    *     o-o       o-o                           o-o               o-o      
    *     |         |                             |                 |        
    *   o-o         o-o               o-o o-o   o-o             o-o o-o      
    *   |           |                 |   |     |               |   |        
    * o-o           o-o           o-o o---o     o-o           o-o   o-o      
    * |             |             |   |         |             |     |        
    * O             O             O===O         O             O=====O        
    *                                                                        
    * 1:4           7:1           1:1 2:2       8:1           1:2 3:1        
    *                                                                        
    * 16            17            18            19            20             
    *                                                                        
    *                                                                        
    *                   o-o                                                  
    *                   |                                                    
    *       o-o         o-o       o-o o-o         o-o         o-o            
    *       |           |         |   |           |           |              
    * o-o o-o           o-o       o---o           o-o o-o     o-o o-o        
    * |   |             |         |               |   |       |   |          
    * o-o o-o       o-o o-o       o-o           o-o   o-o     o---o          
    * |   |         |   |         |             |     |       |              
    * O===O         O===O         O             O=====O       O              
    *                                                                        
    * 2:1 4:1       1:1 5:1       9:1           1:3 2:1       3:2            
    *                                                                        
    * 21            22            23            24            25             
    *                                                                        
    *                                                                        
    *                                               o-o                      
    *                                               |                        
    *         o-o       o-o               o-o       o-o               o-o    
    *         |         |                 |         |                 |      
    *     o-o o-o   o-o o-o         o-o o-o     o-o o-o           o-o o-o    
    *     |   |     |   |           |   |       |   |             |   |      
    * o-o o===o-o   o---o         o-o   o-o     o===o-o       o-o o-o o-o    
    * |   |         |             |     |       |             |   |   |      
    * O===O         O             O=====O       O             O===O===O      
    *                                                                        
    * 1:1 6:1       2:3           1:2 4:1       10:1          1:1 2:1 3:1    
    *                                                                        
    * 26            27            28            29            30             
    *                                                                        
    *                                                                        
    * o-o                                                                    
    * |                                                                      
    * o-o             o-o             o-o             o-o                    
    * |               |               |               |                      
    * o-o             o-o             o-o           o-o       o-o   o-o      
    * |               |               |             |         |     |        
    * o-o             o-o         o-o o-o           o-o       o-o o-o        
    * |               |           |   |             |         |   |          
    * o-o           o-o           o-o o-o       o-o o-o       o-o o-o        
    * |             |             |   |         |   |         |   |          
    * O             O             O===O         O===O         O===O          
    *                                                                        
    * 11:1          1:5           2:1 5:1       1:1 7:1       3:1 4:1        
    *                                                                        
    * 31            32            33            34            35             
    *                                                                        
    *                                                                        
    *                                   o-o                                  
    *                                   |                                    
    *                 o-o o-o           o-o             o-o     o-o o-o      
    *                 |   |             |               |       |   |        
    *   o-o o-o o-o o-o   o-o         o-o       o-o o-o o-o     o-o o-o      
    *   |   |   |   |     |           |         |   |   |       |   |        
    * o-o   o---o   o=====o-o     o-o o-o       o-o o===o-o   o-o   o-o      
    * |     |       |             |   |         |   |         |     |        
    * O=====O       O             O===O         O===O         O=====O        
    *                                                                        
    * 1:2 2:2       12:1          1:1 8:1       2:1 6:1       1:3 3:1        
    *                                                                        
    * 36            37            38            39            40             
    *                                                                        
    * In these Figures, "extended lines of identity" like o===o
    * indicate identified nodes and capital O is the root node.
    * The rote height in gammas is found by finding the number
    * of graphs of the following shape between the root and one
    * of the highest nodes of the tree:
    * o--o
    * |
    * o
    * A sequence like this, that can be regarded as a nonnegative integer
    * measure on positive integers, may have as many as 3 other sequences
    * associated with it. Given that the fiber of a function f at n is all
    * the domain elements that map to n, we always have the fiber minimum
    * or minimum inverse function and may also have the fiber cardinality
    * and the fiber maximum or maximum inverse function. For A109301, the
    * minimum inverse is A007097(n) = min {k : A109301(k) = n}, giving the
    * first positive integer whose rote height is n, the fiber cardinality
    * is A109300, giving the number of positive integers of rote height n,
    * while the maximum inverse, g(n) = max {k : A109301(k) = n}, giving
    * the last positive integer whose rote height is n, has the following
    * initial terms: g(0) = { } = 1, g(1) = 1:1 = 2, g(2) = 1:2 2:2 = 36,
    * while g(3) = 1:36 2:36 3:36 4:36 6:36 9:36 12:36 18:36 36:36 =
    * (2 3 5 7 13 23 37 61 151)^36 = 21399271530^36 = roughly
    * 7.840858554516122655953405327738 x 10^371. 

A111795

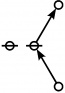
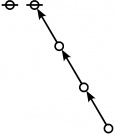
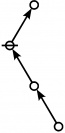
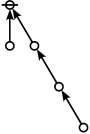
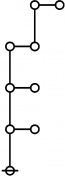
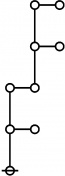
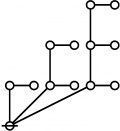
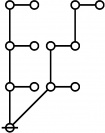
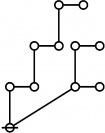
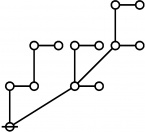
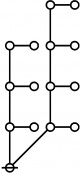
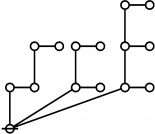
• A111795

JPEG

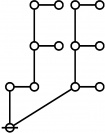
\(\begin{array}{l} \varnothing \\ 1 \end{array}\)	\(\begin{array}{l} 1\!:\!1 \\ 2 \end{array}\)	\(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\)	\(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\)	\(\begin{array}{l} 3\!:\!1 \\ 5 \end{array}\)
\(\begin{array}{l} 4\!:\!1 \\ 7 \end{array}\)	\(\begin{array}{l} 1\!:\!3 \\ 8 \end{array}\)	\(\begin{array}{l} 5\!:\!1 \\ 11 \end{array}\)	\(\begin{array}{l} 1\!:\!4 \\ 16 \end{array}\)	\(\begin{array}{l} 7\!:\!1 \\ 17 \end{array}\)
\(\begin{array}{l} 8\!:\!1 \\ 19 \end{array}\)	\(\begin{array}{l} 11\!:\!1 \\ 31 \end{array}\)	\(\begin{array}{l} 1\!:\!5 \\ 32 \end{array}\)	\(\begin{array}{l} 16\!:\!1 \\ 53 \end{array}\)	\(\begin{array}{l} 17\!:\!1 \\ 59 \end{array}\)

ASCII

 Example

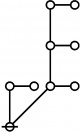
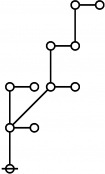
    * Tables of Rotes and Primal Codes for a(1) to a(9)
    *                                                              
    *                                                 o-o          
    *                                                 |            
    *                           o-o     o-o     o-o   o-o       o-o
    *                           |       |       |     |         |  
    *             o-o     o-o   o-o   o-o       o-o   o-o     o-o  
    *             |       |     |     |         |     |       |    
    *       o-o   o-o   o-o     o-o   o-o     o-o     o-o   o-o    
    *       |     |     |       |     |       |       |     |      
    * O     O     O     O       O     O       O       O     O      
    *                                                              
    * { }   1:1   2:1   1:2     3:1   4:1     1:3     5:1   1:4    
    *                                                              
    * 1     2     3     4       5     7       8       11    16     
    *                                                              

A111800

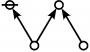
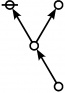
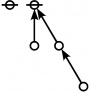
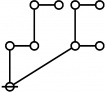
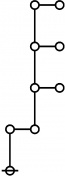
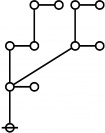
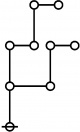
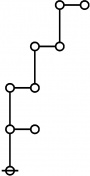
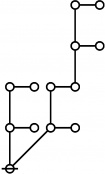
• A111800

TeX + JPEG

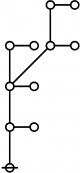
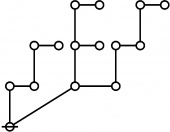
\(\text{Writing}~ \operatorname{prime}(i)^j ~\text{as}~ i\!:\!j, 2500 = 4 \cdot 625 = 2^2 5^4 = 1\!:\!2 ~~ 3\!:\!4 ~\text{has the following rote:}\)

\(\text{So}~ a(2500) = a(1\!:\!2 ~~ 3\!:\!4) = a(1) + a(2) + a(3) + a(4) + 1 = 1 + 3 + 5 + 5 + 1 = 15.\)

ASCII

 Example

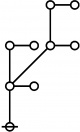
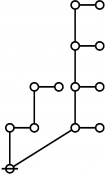
    * Writing prime(i)^j as i:j and using equal signs between identified nodes:
    * 2500 = 4 * 625 = 2^2 5^4 = 1:2 3:4 has the following rote:
    *                
    *       o-o   o-o
    *       |     |  
    *   o-o o-o o-o  
    *   |   |   |    
    * o-o   o---o    
    * |     |        
    * O=====O        
    *                
    * So a(2500) = a(1:2 3:4) = a(1)+a(2)+a(3)+a(4)+1 = 1+3+5+5+1 = 15.